Java Data Structure and Algorithm
Java 数据结构与算法
大 O 表示法:比较的是操作数,指出算法运行时间的增速。
如何选择数组和链表:
- 增删情况较多的需求下选择链表。
- 改查情况较多的情况下选择数组。
选择排序
- 每次循环找当前查询数组中最小或者最大元素的索引
- 得到索引之后,将索引位置的值与顺序放置位置交换
- 直至循环结束
🗝特点:找到最小或者最大元素的索引,通过索引进行元素交换。
1 | |
递归
🗝递归的两个条件:
- 基线条件:防止死循环
- 递归条件:自己调用自己
1 | |
链表 队列
双向链表
单向链表的缺点:
- 只能一个方向查找
- 不能实现自我删除,需要辅助节点
双向链表的遍历:可以向前和向后遍历
添加:先找到最后节点,temp.next = newNode; newNode.pre = temp
修改:
删除:实现自我删除: node5.pre.next= node5.next; node5.next.pre = node5.pre
单向环形链表 约瑟夫问题
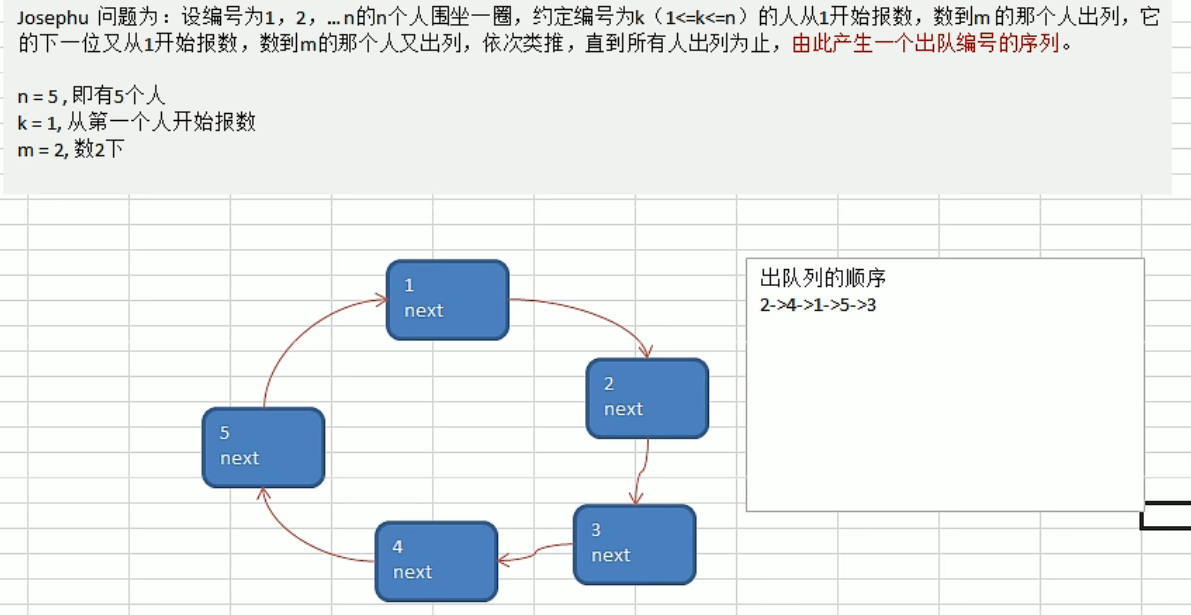
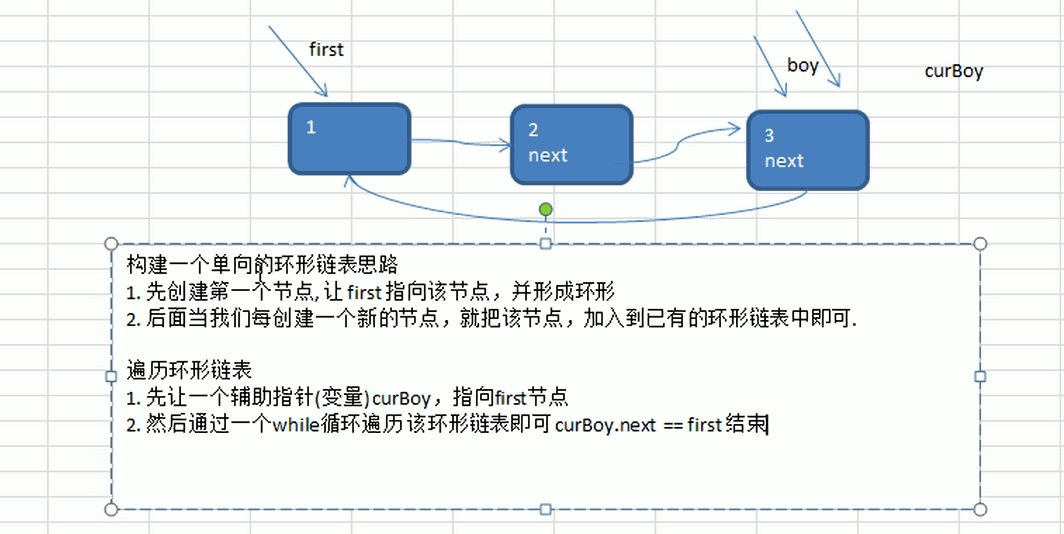
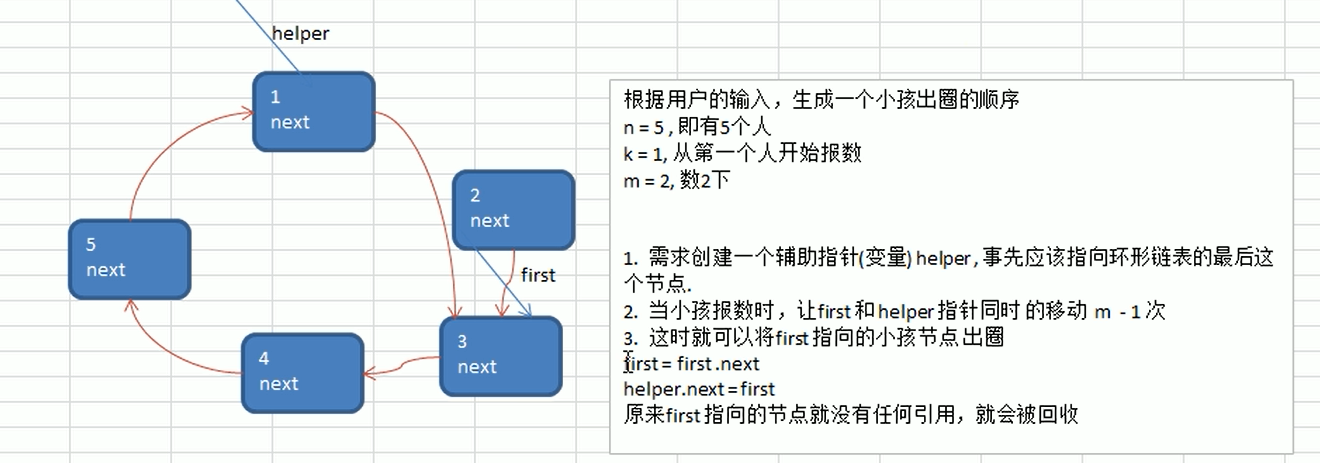
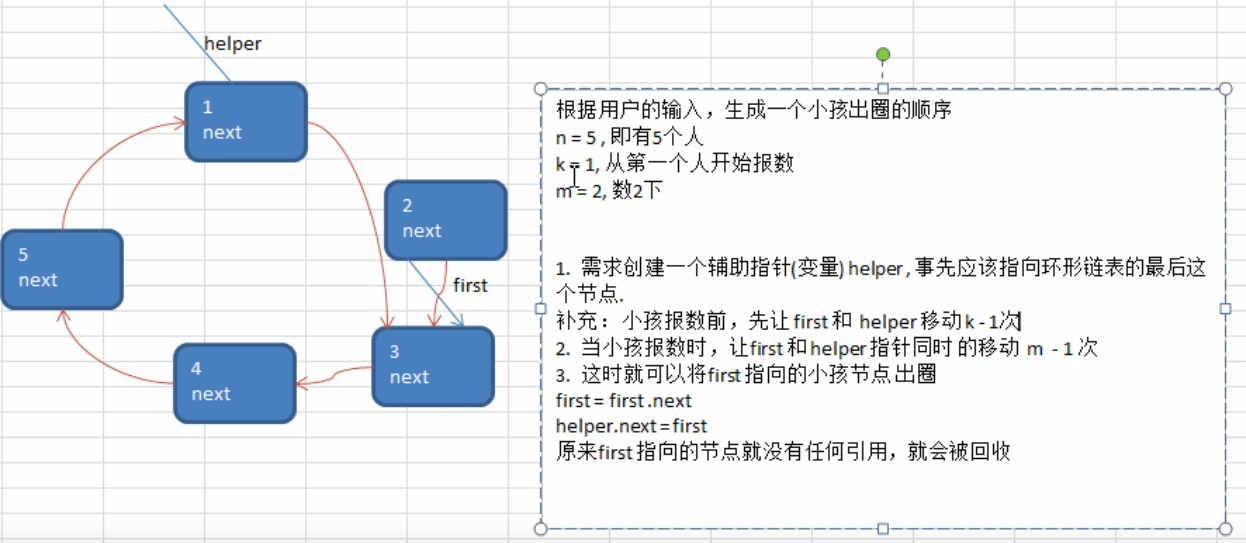
1 | |
栈
FIFO
应用场景

1 | |
栈实现综合计算器
编写特点:
- 写MyStack在继承Java 提供的 Stack
- 在MyStack 中提供运算符优先级判断,使用数字表示 * :2,+:1
- 在MyStack 中提供符号判断的方法
- 在MyStack 中提供运算方法
- 使用字符扫描字符串表达式根据扫描到的运算符判断当前是否可以进行运算
- 主要 char 和 int 转换时 char (‘7’,’0‘)(70)可能是两个字符,需要使用字符串配合符号判断对70进行拼接
- 扫描越界问题

中缀表达式转后缀表达式
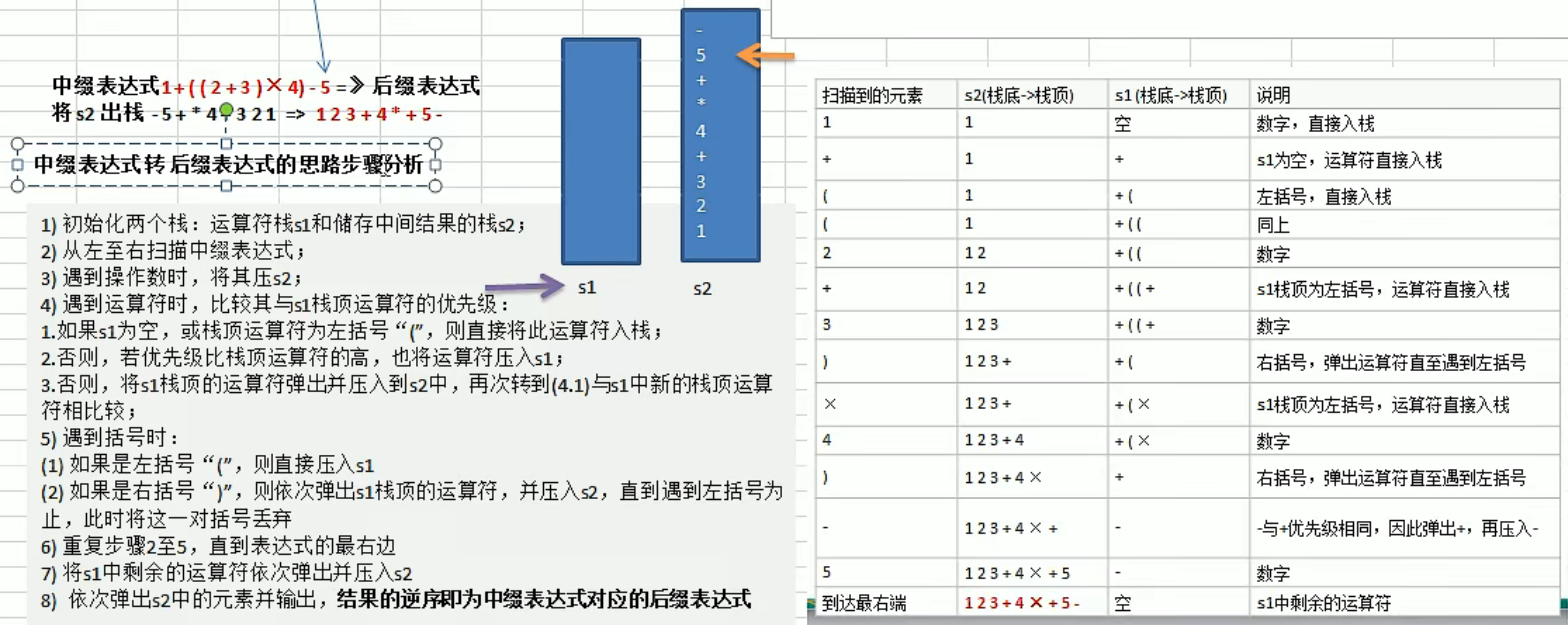
1 | |
递归


迷宫问题:

编写思路
- 确定策略:先上? 上-》下-》左-》右 去尝试
- 设置递归退出条件,即走到了目的地
- 先占位置 map/[ i ][ j ] = 2 ,然后走;
- 在进入迷宫时尝试探索下一步,如果下一步可行返回 true 继续递归
- 在遇见当前路是墙:1, 走过的:2, 死路:3 就返回 false
1 | |
八皇后问题


编写思路:
- 拆分问题
- 设置输出函数输出每次的找的结果
- 设置check 函数检查防止是否符合要求 (对于斜线上的要巧用函数的思维,即斜率为1 or -1)
- 设置放置函数放置皇后
- 先占位置 array[n] = i; 再判断 if(isNotConflict(n)
- 在编写放置皇后函数时
- 设置递归退出条件
- 由于每次每列只有一个皇后,即 n th 列数== n th 皇后
- 在每列放置皇后时,如果当前位置不冲突,就去递归检查下一行 or 下一个皇后
- 如果当前列中当前的位置不对,则循环 check 下一个位置,如果 check(n+1)没有找到,退出 if 条件,尝试 n 行中的下一个位置
1 | |
排序算法
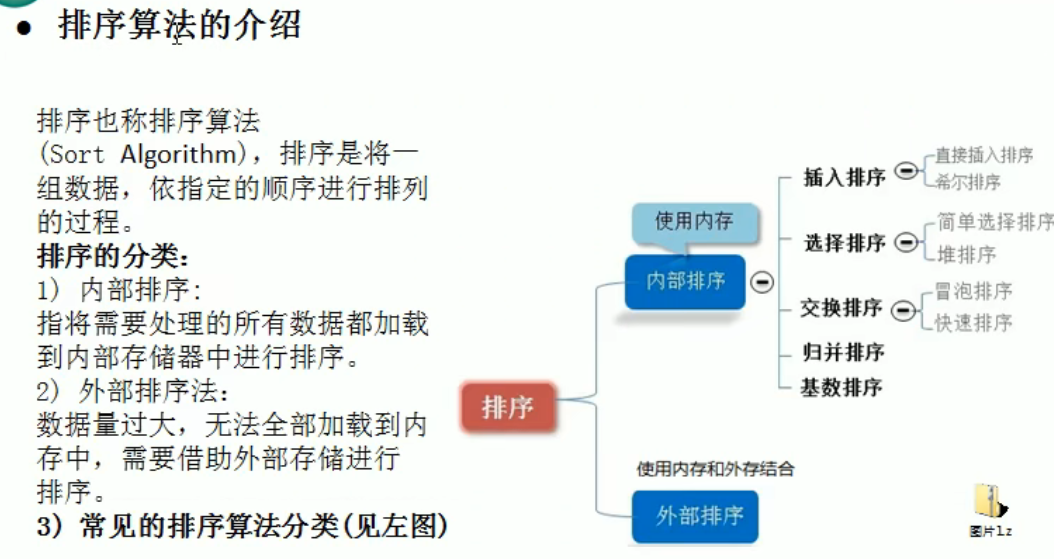
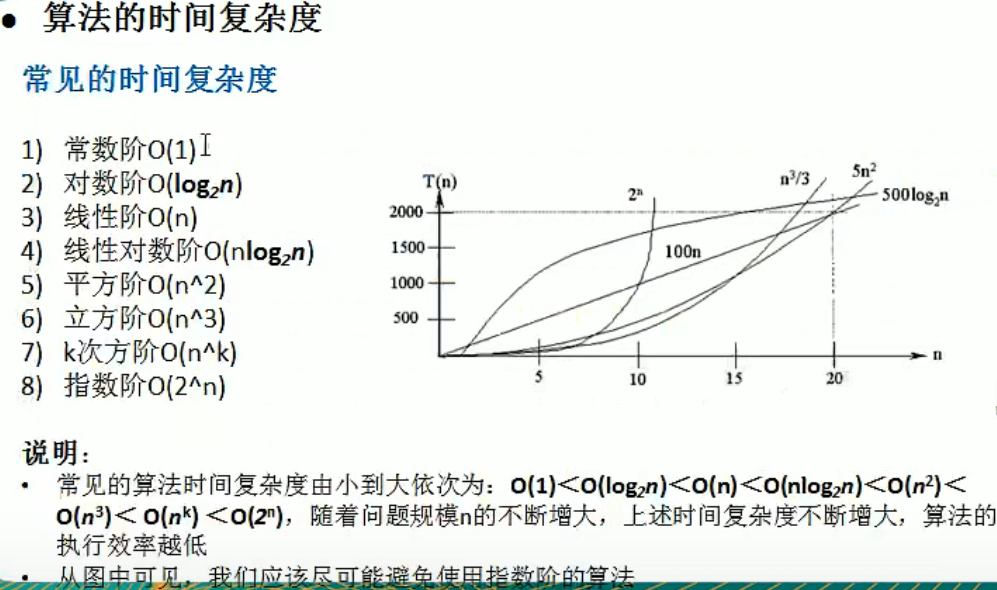
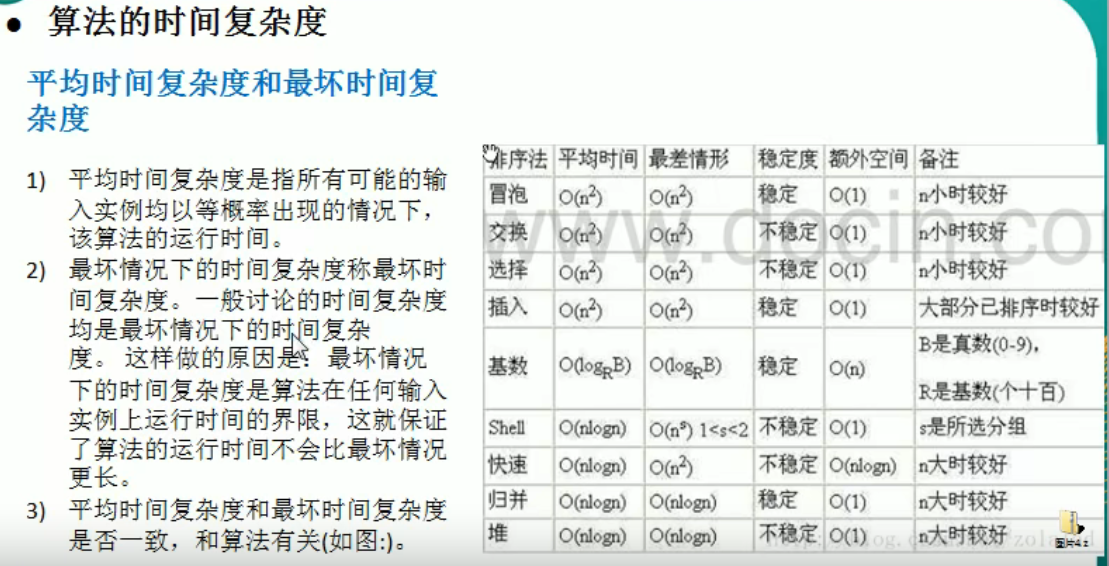
冒泡排序


编写思维:
- 相邻元素之间发生交换
- 大循环次数 = 元素的个数 - 1 《== 每次大循环都会确定最大的一个数的位置,知道确定第二位置,就结束了(第一个自动就是最小)
- 小循环的次数 = 待排元素的个数 - 1 《== 待排元素的个数和大循环的次序有关, 即 元素个数 -( 0, 1, 2, 3, … )
- 优化:一次循环中一次交换都没有发生过,即数组已经有序。(每次都是从左至右依次两两比较,即 1< 2 ,2 < 3 ==》1 < 2 < 3)
1 | |
选择排序
由于只需要交换最小的元素,交换次数的减小使其性能由于冒泡排序
编写思路:
- 只是找到最小值的时候交换
- 每次找到当前待排数组中最小的数进行交换
- 需要发生交换就需要记录当前最小值及其index
- 大循环次数 = 元素个数 - 1 《= 需要第一个位置和后面的位置进行比较
- 小循环需要从 i + 1 开始《= 即第一个待排位置的下一位

1 | |
插入排序
编写思路:
- 两个list,一个有序一个无序
- 每次都从大循环中取出一个元素,记录待插入元素(insertValue)及其前一个位置(insertIndex)
- 插入之前的有序表,从有序表的最后一位开始比较知道找到
- 第一次,第一个元素就是有序的,后面其他元素是无序的
- 中间比较时,有序表中较大的数需要移动位置为待插入的数(insertValue)腾出空间,使用 insertIndex 比较并记录位置。

1 | |
希尔排序
其目的是为了减少排序中的交换问题


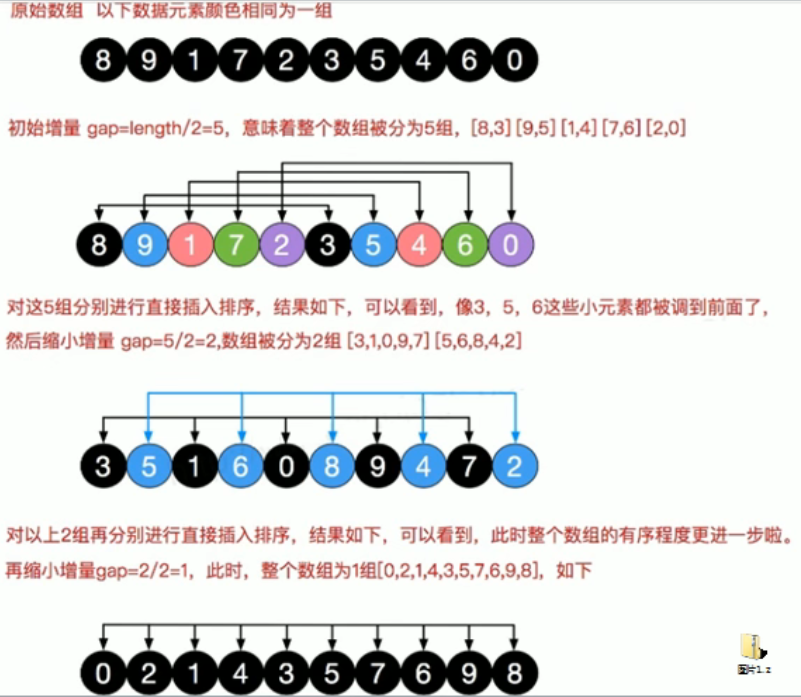
交换式:
1 | |
测试之后:时间变慢 14s 左右(8w nums),主要是交换的次数变多了
移动法
快了很多 1s (8w nums)
1 | |
快速排序

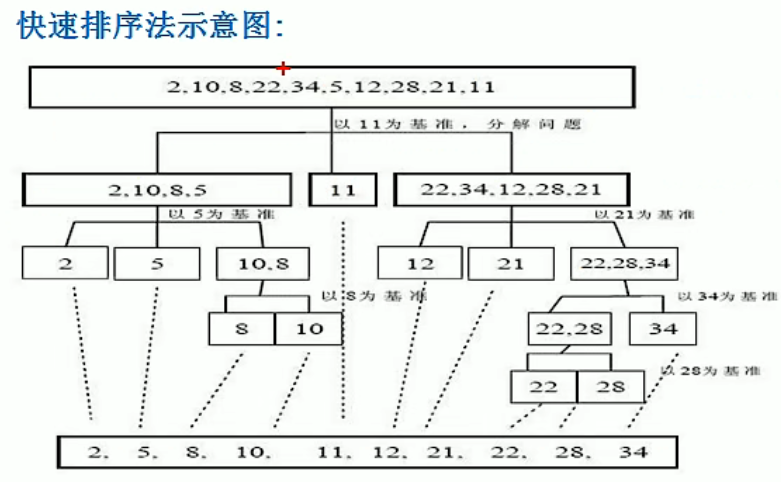
每一次遍历,我们在当前处理的数组上维护四个区域,如下图所示。
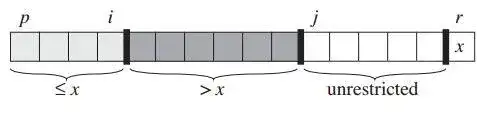
最左侧是小于等于主元的元素,中间左侧是大于主元的元素,中间右侧是待遍历的元素,最右侧是主元 ![[公式]](/img/loading.gif)
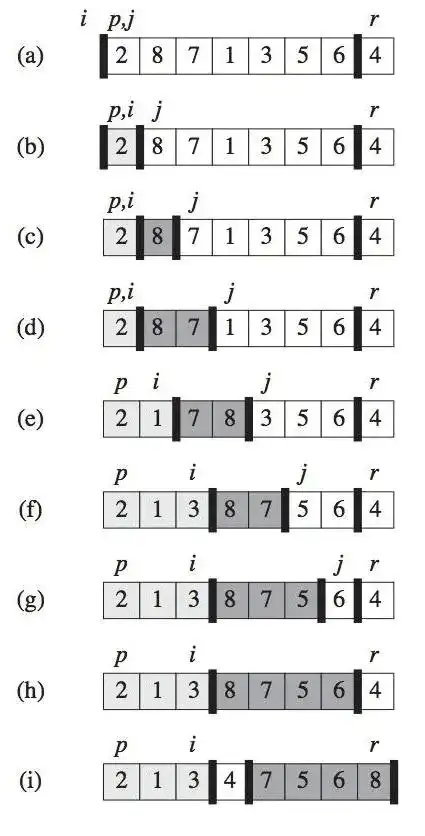
每一趟遍历之前,选取最后一个数作为主元x,通过遍历整个序列,把“无限制”区域的数放到区域一或区域二中。下图展示了给定序列的一趟快速排序过程。
编写思路:
- 确定递归的退出条件
- 确定排序的4个区域
- 给每个区域确定index
- p, r 位置不变用于后面递归传递数组位置
- i:表示比 x 小的数组的最后一个元素的 index
- j: 表示unrestricted 区域首元素的index
- 每次 j 都会增加,当 unrestricted 元素小于 x 时 ,则与 i+1 的值即比 x 大的数组的第一个元素交换,由于每次 j 都会增加,则 >x 的数组个数和元素并没有受到影响。
- 完成一次扫描之后就递归操作
1 | |
归并排序

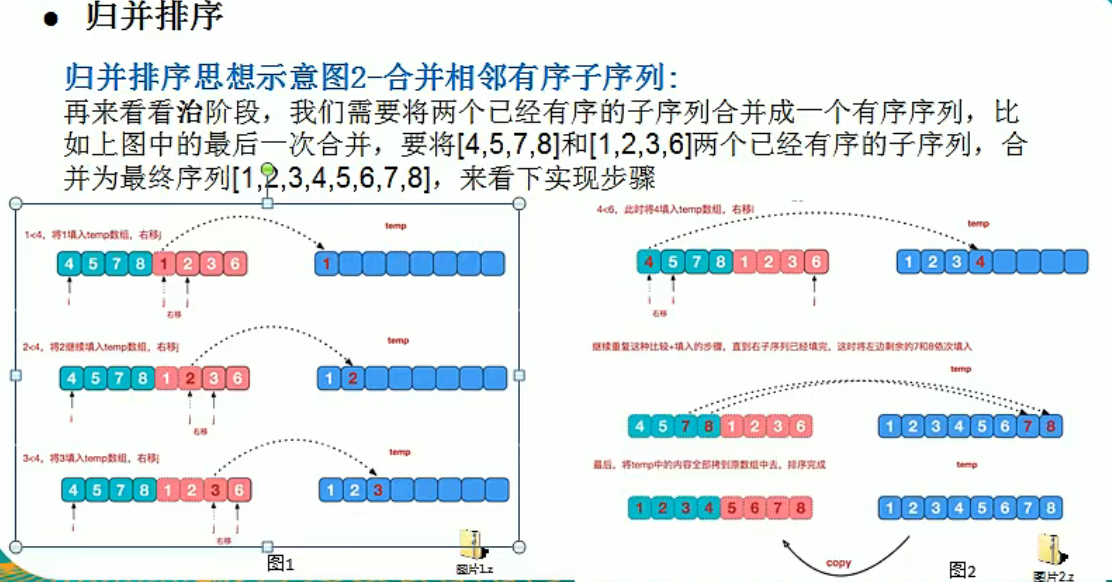
编写思路
- 差分方法
- 在分中要设置递归退出条件
- 并中考虑复制方法
1 | |
基数排序


编写思路:
- 确定最大数的位数
- 需要设置二位数组表示桶
- 需要设置一维数组记录当前放入桶的数据的个数
- 每次取出数据到原数组时需要将记录个数的数组清空
1 | |

排序对比
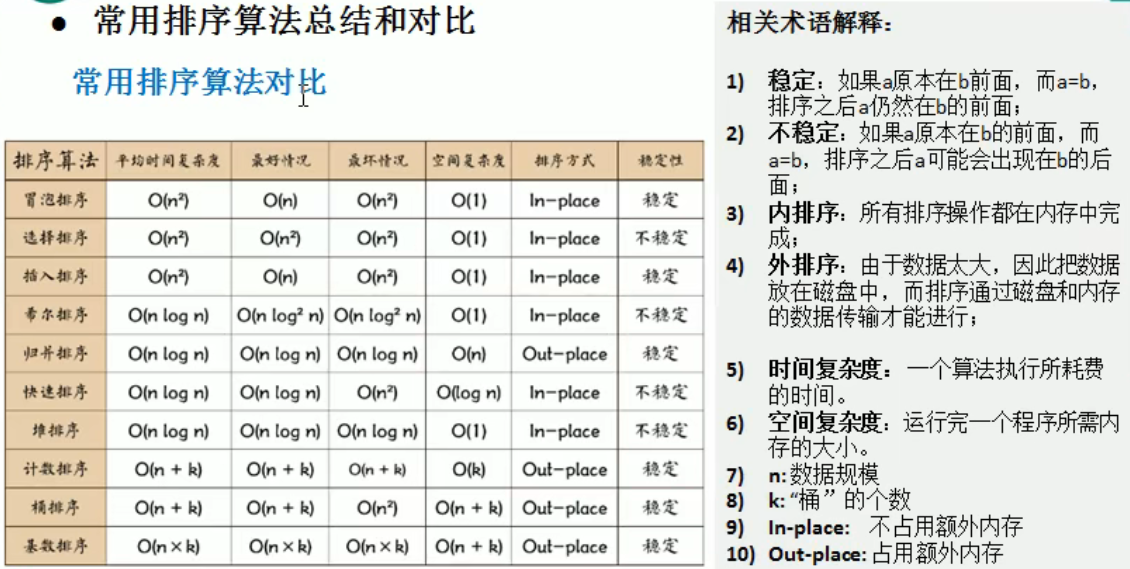
查找算法
二分查找
有序数组中查找
编写思路:
- 确定递归退出条件(1. 没有找到,由于每次递归 mid 值都已经对比过了,再下次设定向左或向右时,需要 -1 or +1,就会出现 left > right,则退出递归,2. 找到了)
1 | |
对于有多个相同值的数组
1 | |
插值查找
自适应的算法,对于关键字分布均匀的查找表来说很快。
在分布不均匀的情况下不一定好于二分查找

1 | |
斐波拉契查找
由于其只涉及加减理论上可能比二分查找要快。
编写思路:
- 设置斐波那契的 index 数组
- 如果查找数组不够需要补充满足斐波那契数组的index值
- 切分查找数组为前 f[n-1]-1 和后 f[n-2]-1 两个部分 f[n]-1 (index) = f[n-1]-1 + f[n-2]-1 + 1 ( 1表示黄金分割位置上的数的个数)
- 则 黄金分割数(mid)= low + f[n-1]-1
- 如果在左边,则 high = mid - 1;新一次的(index) mid = low + f[n-1-1] - 1,即需要 n–
- 如果在右边,则 low= mid + 1; 新一次的(index) mid = low + f[n-1-2] - 1,即 low 已经从黄金分割数左边开始了,然后加上前面部分的开始,需要 n-=2。
- 如果 mid > high,则已经找到了填充数了,则返回 high 即可。


1 | |
哈希表
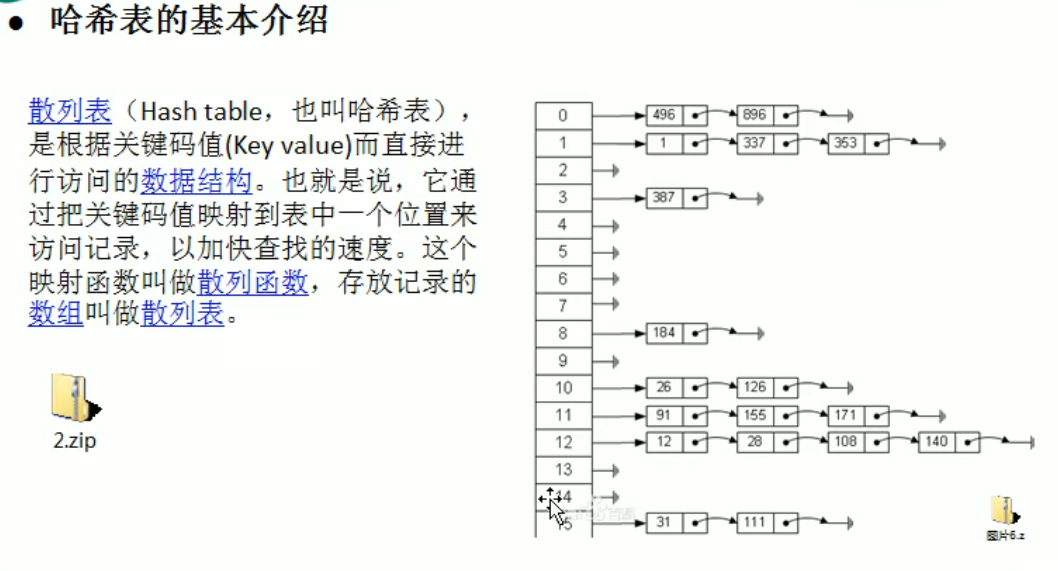
1 | |
Tree
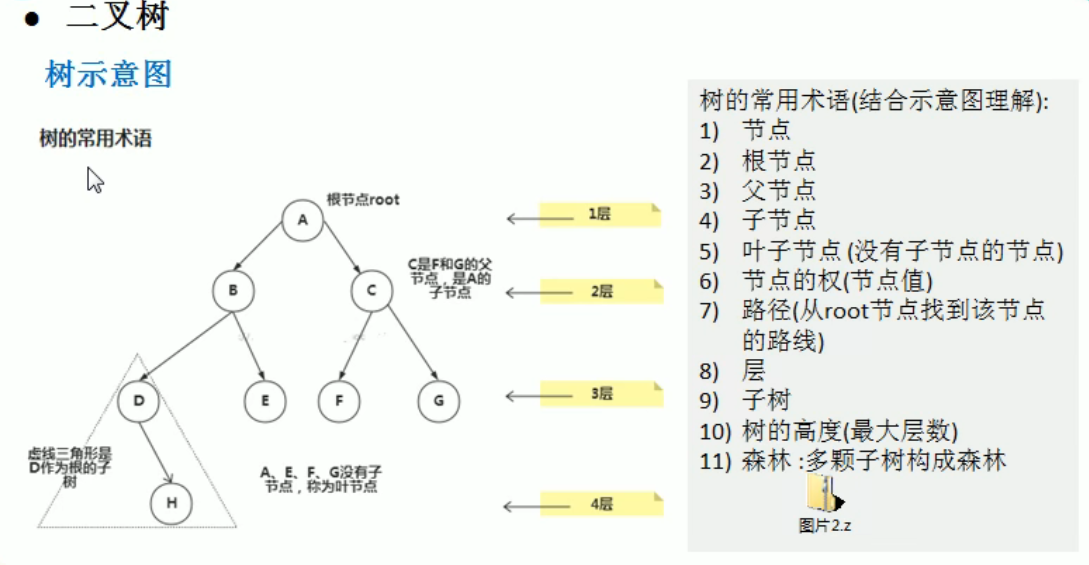
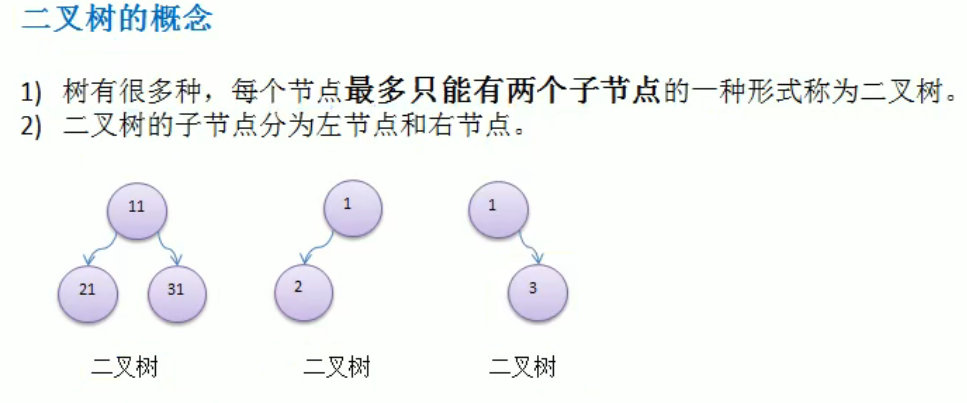
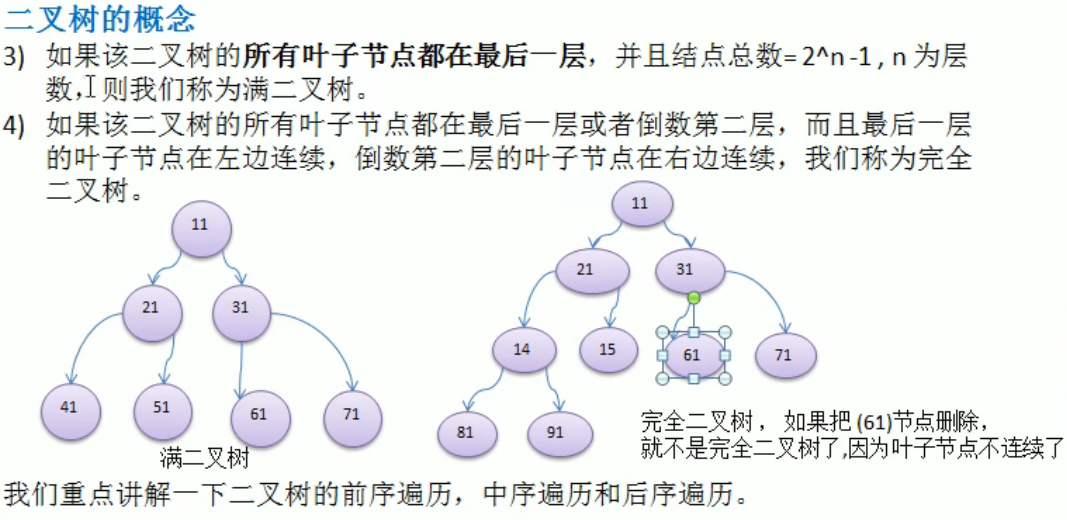

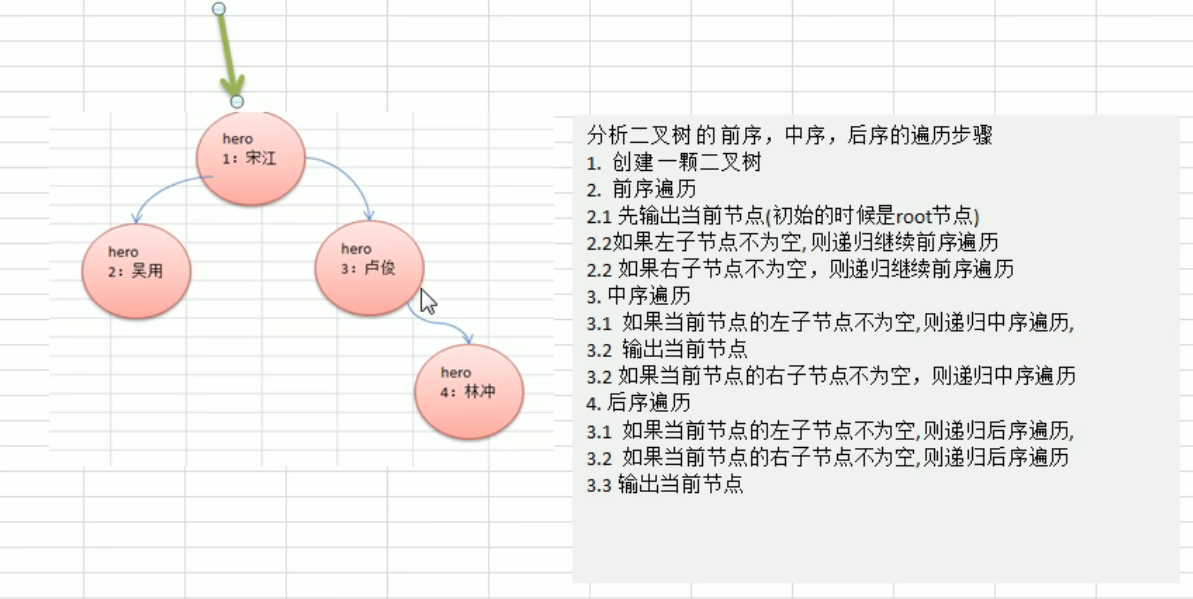
1 | |
前中后序查找
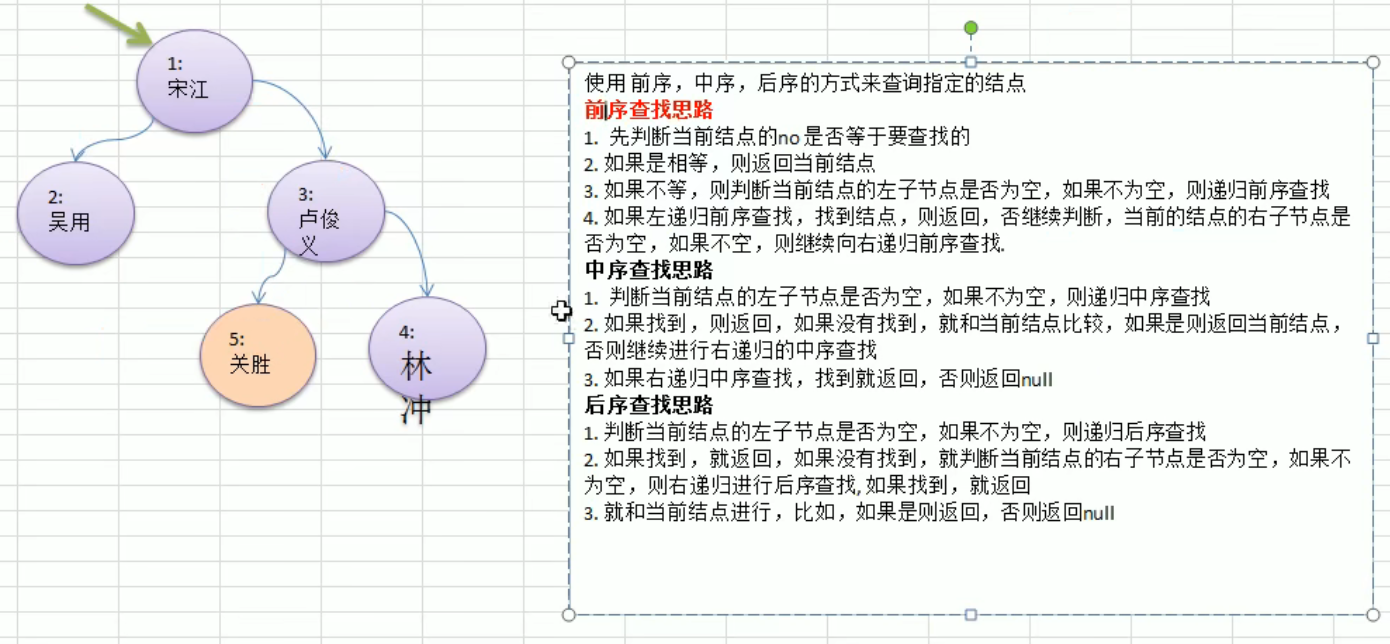
1 | |
删除节点
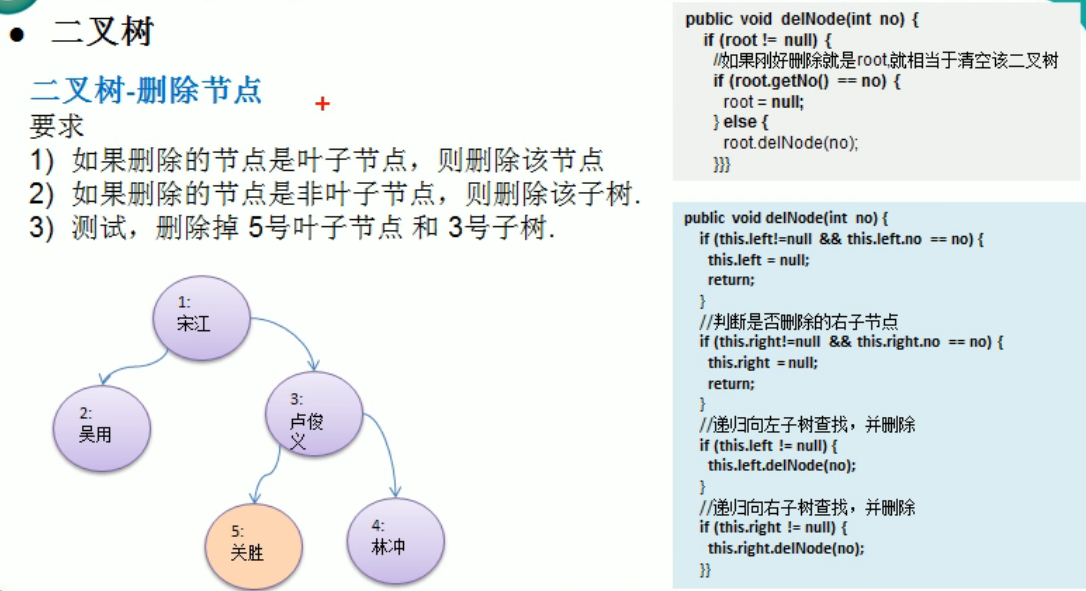
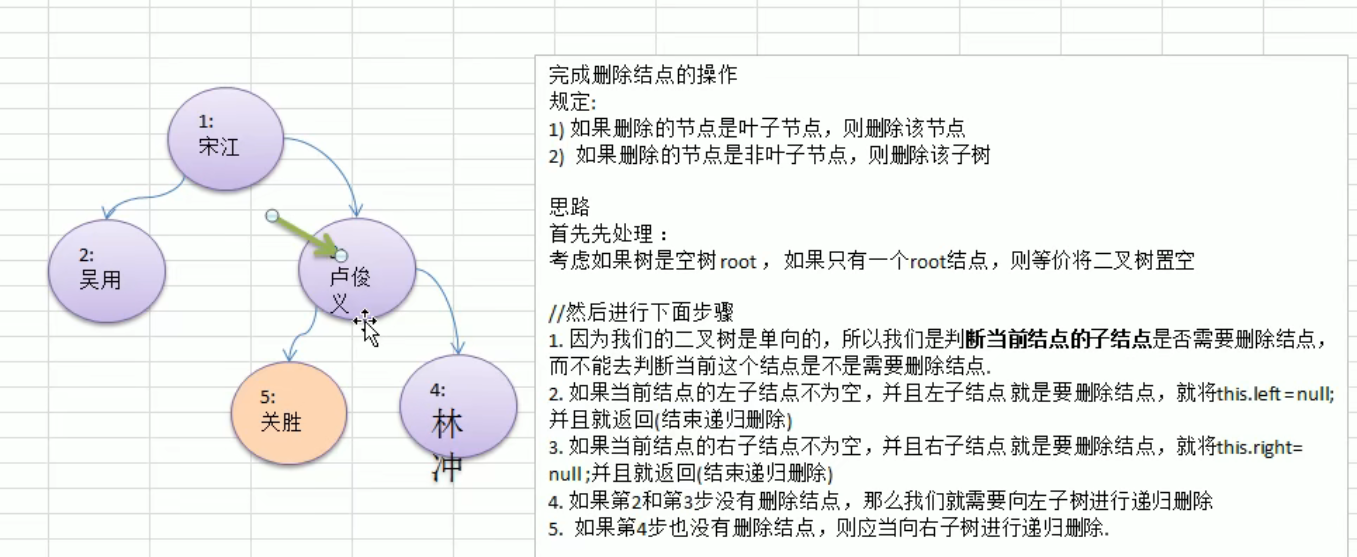
1 | |
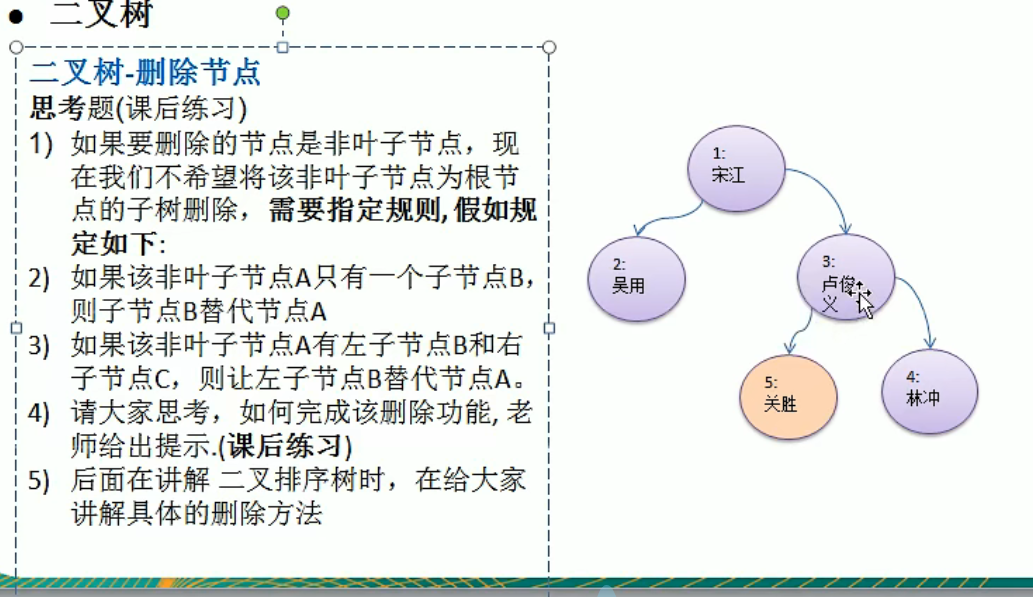
1 | |
顺序存储二叉树
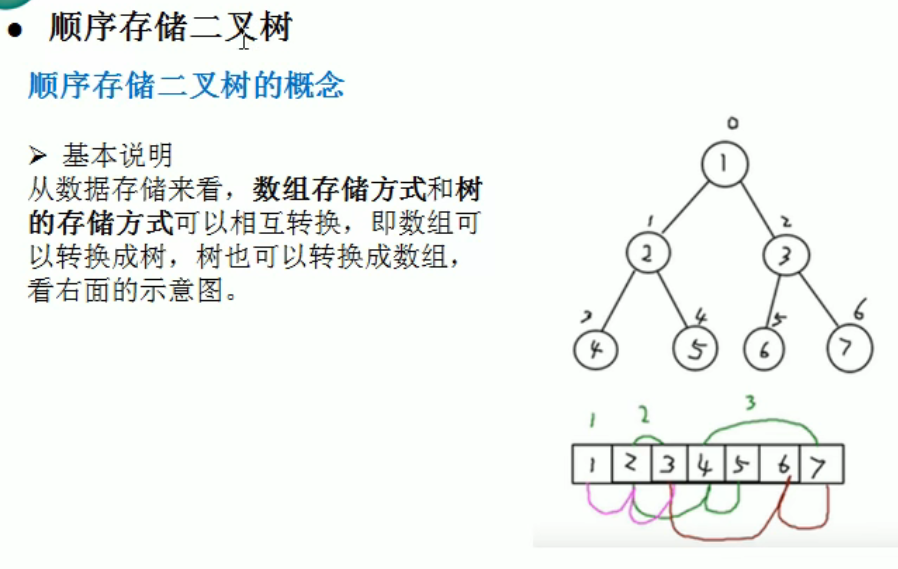

1 | |
线索化二叉树
构建
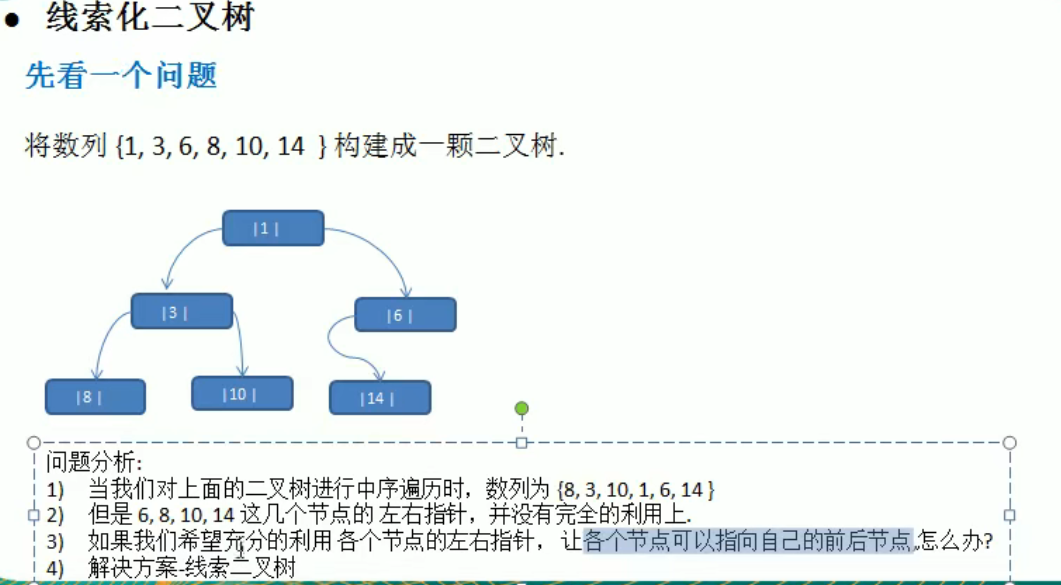

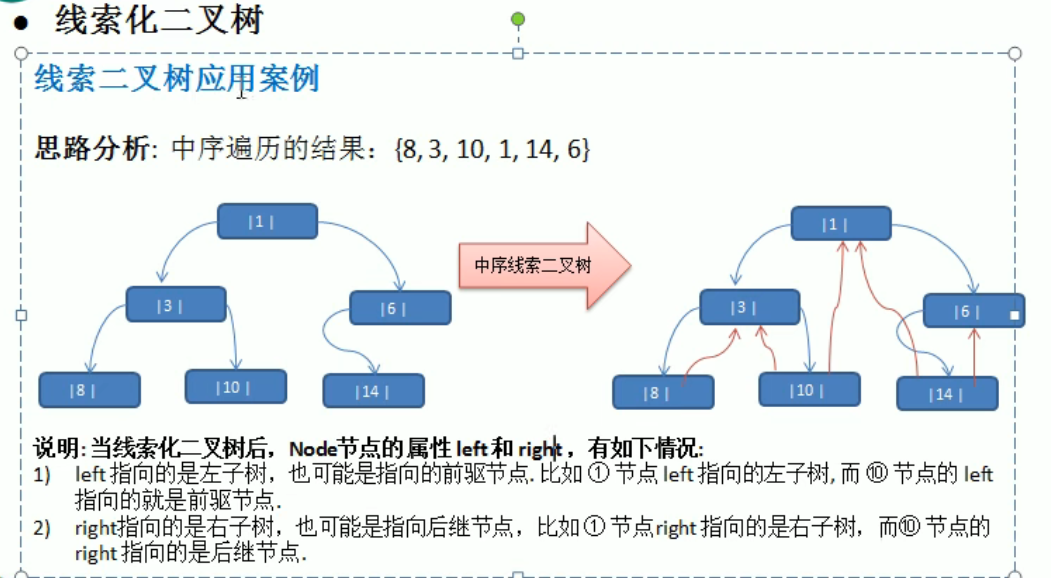
1 | |
遍历
编写思路:
- 确定它是哪种遍历,如中序遍历
- 每次输出前都要找到当前子树的左叶子节点
- 然后输出
- 如果当前的节点有后继节点,循环输出后继节点
- 没有,则将右子节点设为当前节点
1 | |
堆排序
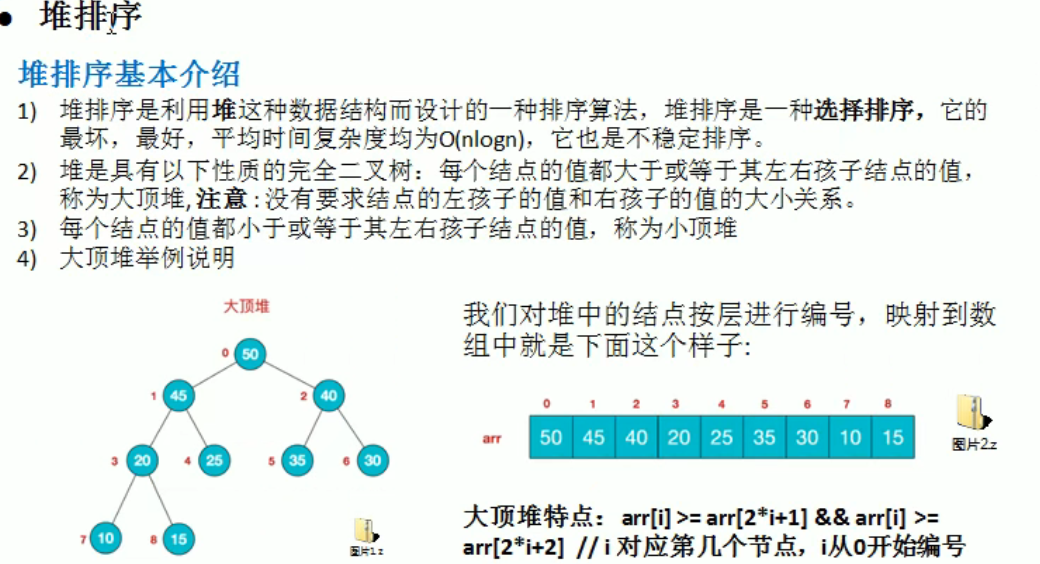
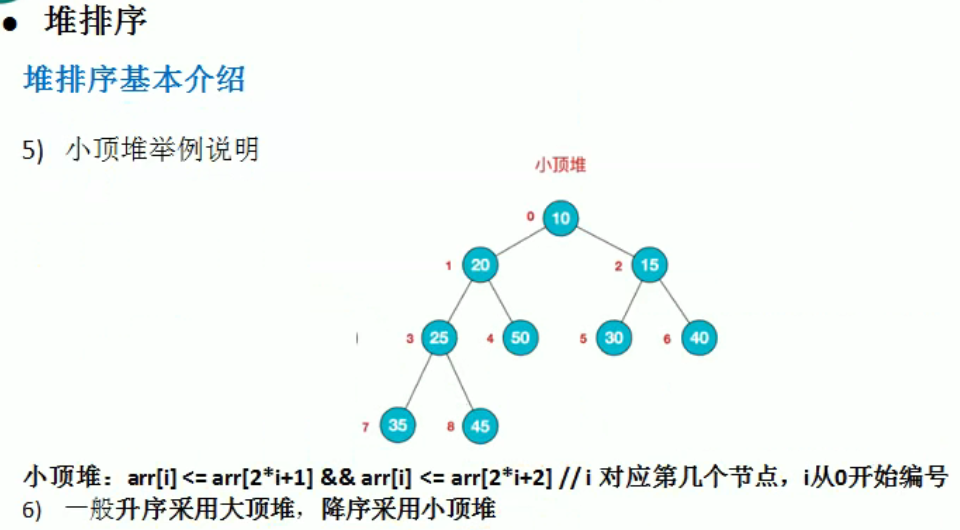

编写思路:
- 根据需求先变成大顶堆还是小顶堆。
- 对树中数据的处理是从左至右,从下至上
- 先编写对 i 节点的子树的处理,先比较其左右字节的,如果是大顶堆,让大的子节点与 i 节点比较,并交换
- 对与完全二叉树层数和节点的关系是 n = 2^(l-1)-1 + m;l:层数;m:最后一层的节点数 n: 节点数
- 如果节点有10个, l = 4, 从倒数第二层开始处理子树数据则 i 节点 = 10/2 -1
- 处理完之后从数中 pop 出根节点 (与最后一个叶节点交换)
- 然后从顶部开始重新整理数,因为每次只 pop 一个根节点,只有一个数据发生了变化,所以可以从顶部直接循环,即如果和左子节点交换,右子节点为父节点的子树一定是有序的。
1 | |
赫夫曼树

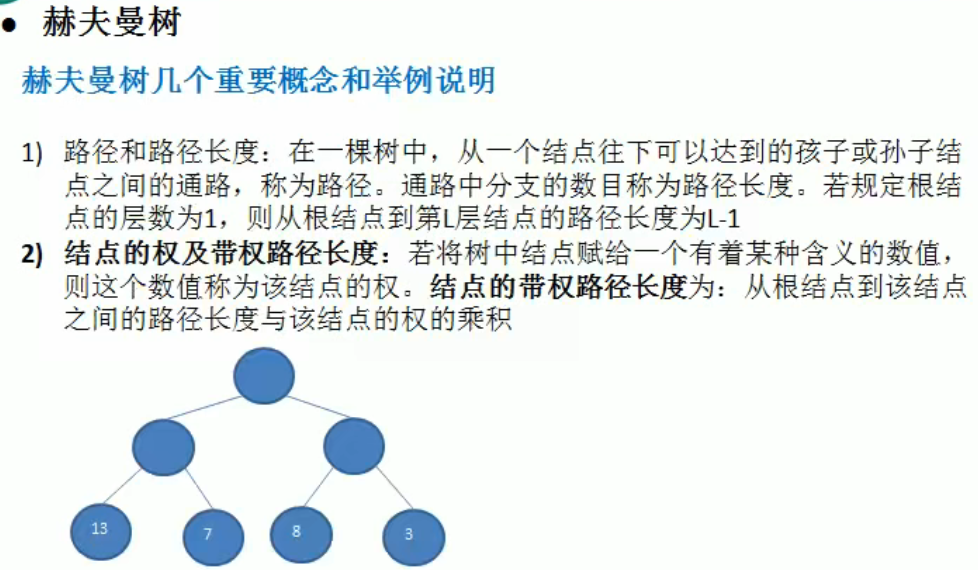
到 13 节点的路径长度是 2, 带权路径长度是 2*13 = 26
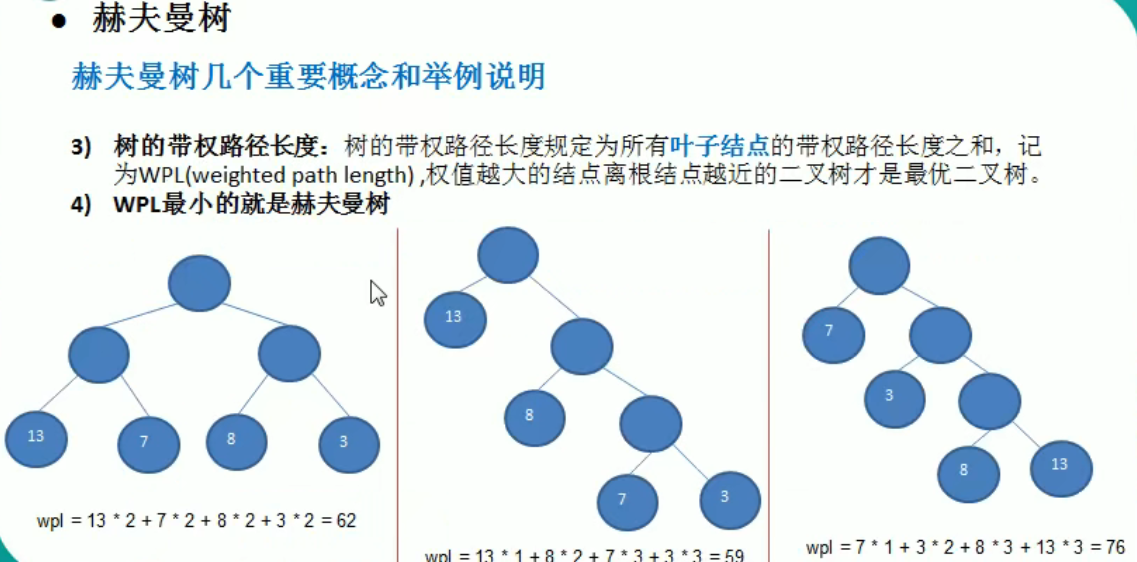

编写思路:
- 对节点排序,如果使用集合的排序方法(Collections.sort(para))需要实现Comparable 接口中的compareTo 方法
- 每次操作前先排序
- 每次生成子树所使用的节点需要从List 中删除并将其父节点放入 list
1 | |
赫夫曼编码





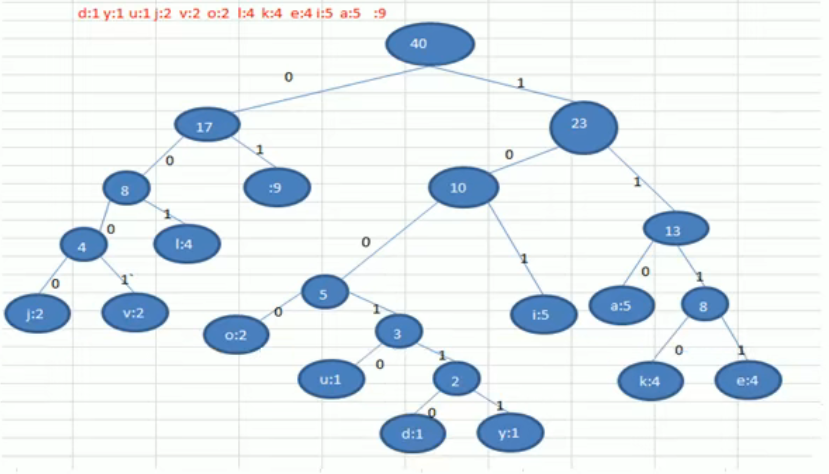

数据压缩
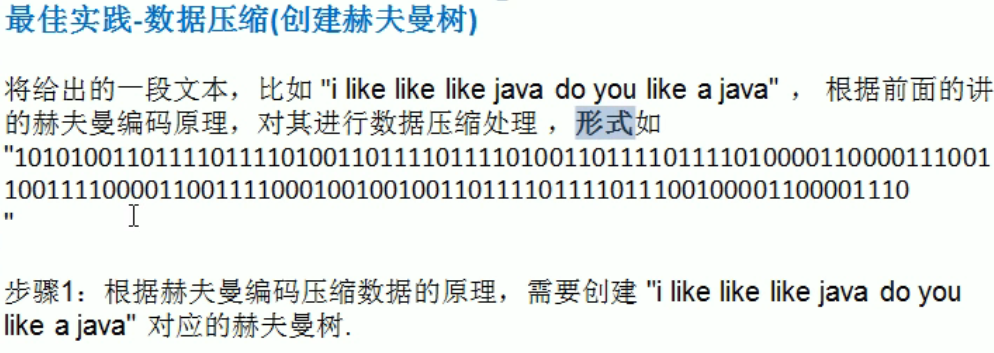

1 | |
小节(注意事项)

二叉排序树


1 | |
删除节点




1 | |
平衡二叉树 AVL 树


左旋转


1 | |
右旋转

1 | |
双旋转


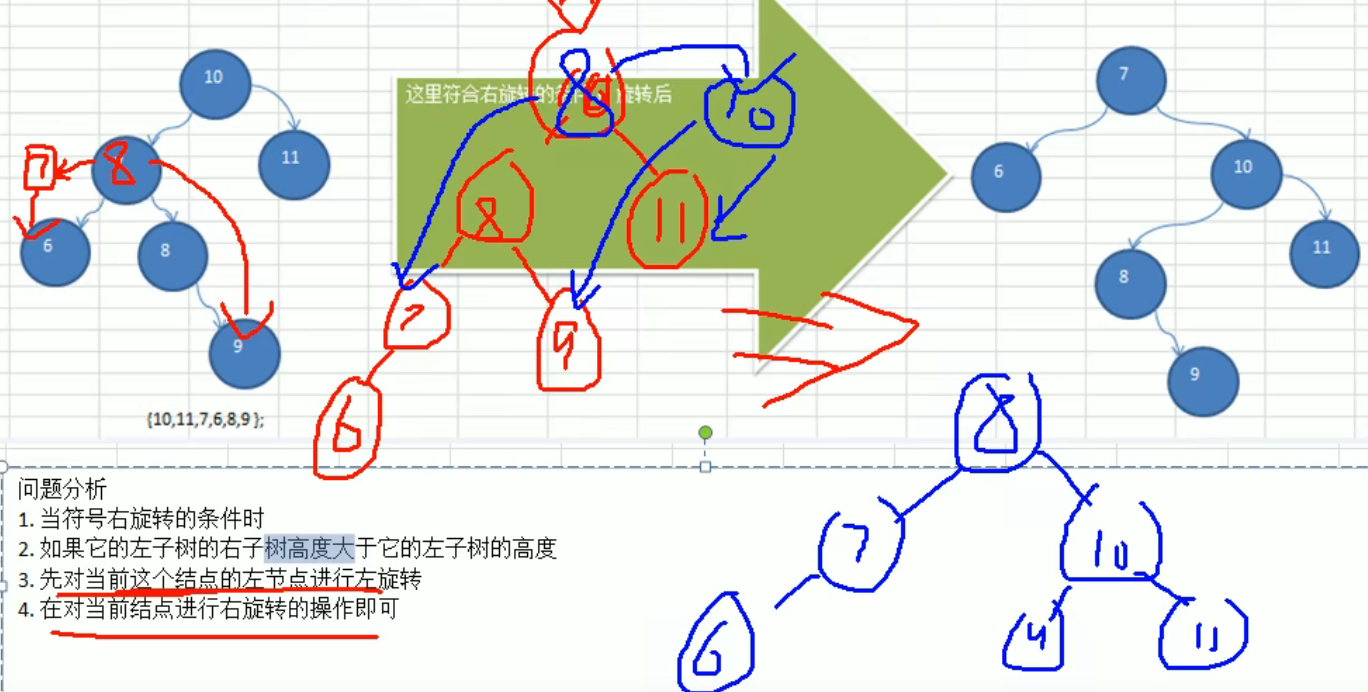
在节点的 add 方法中加这几行代码:
注意:
1 | |
多路查找树
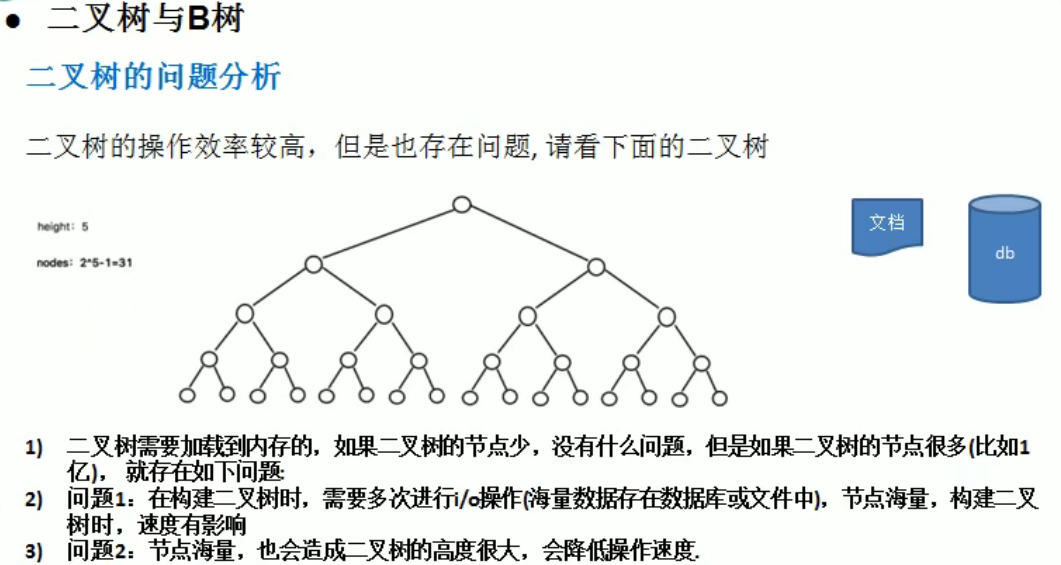
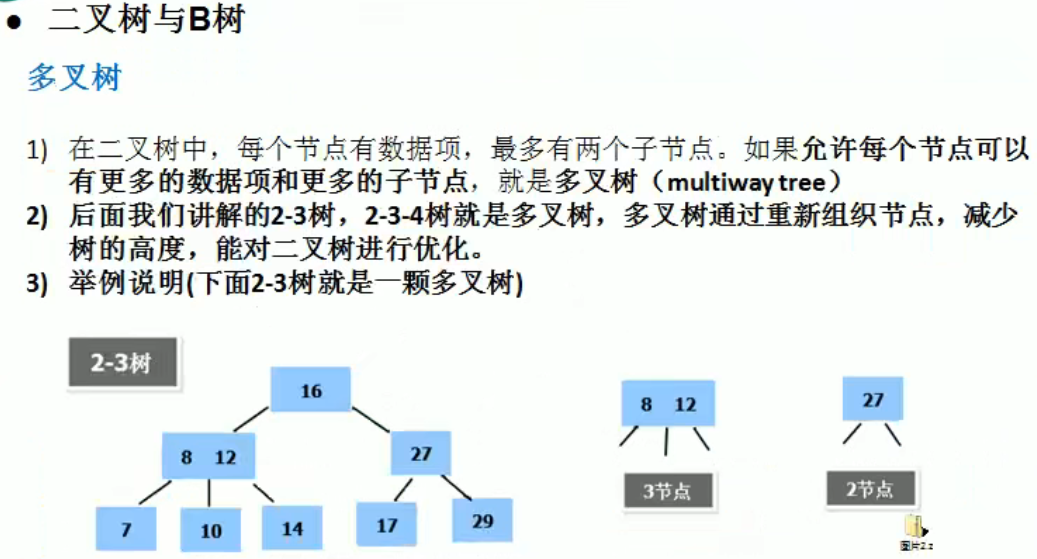
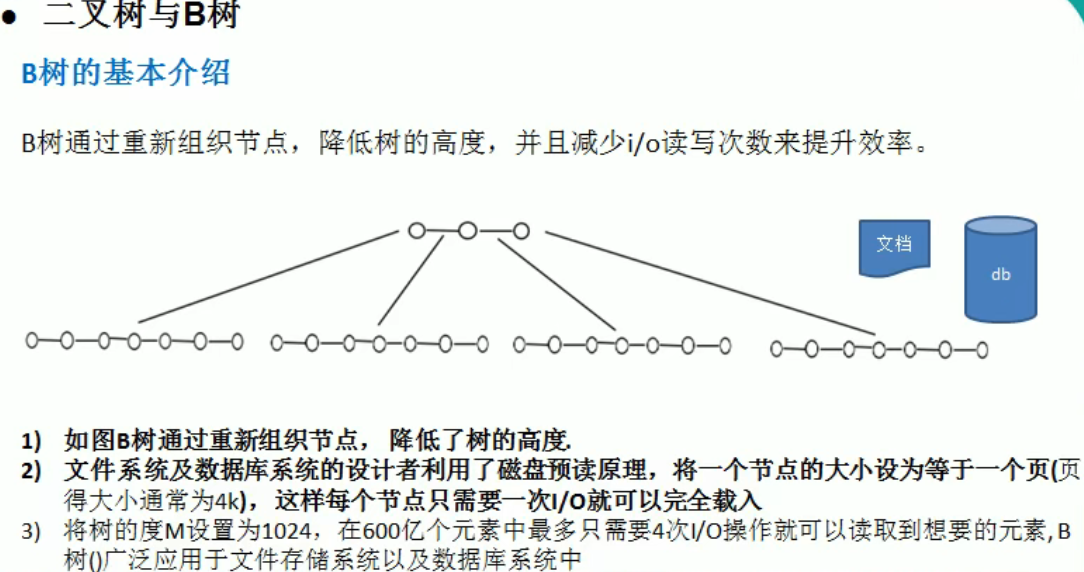

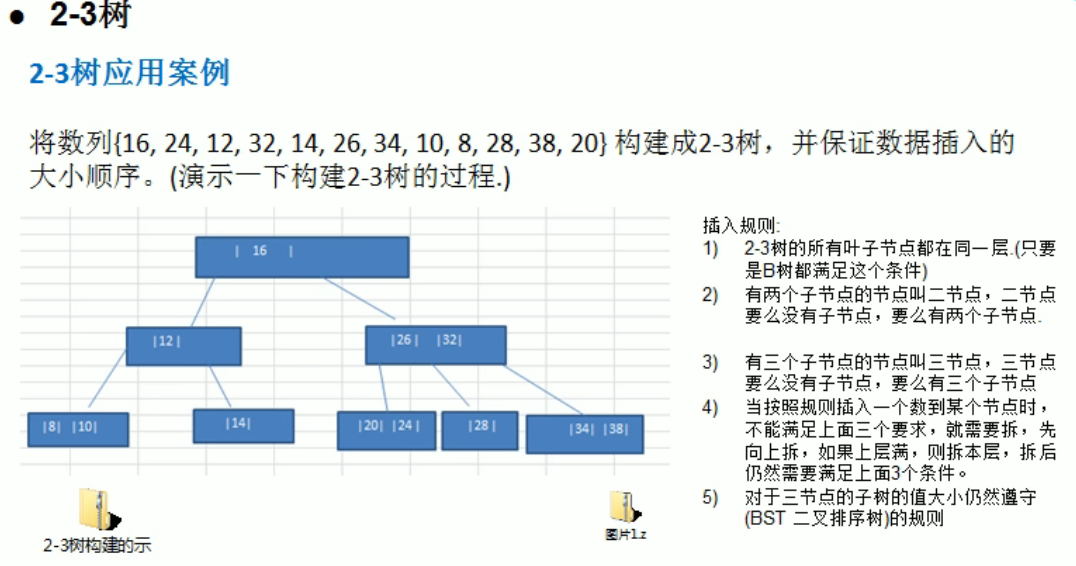
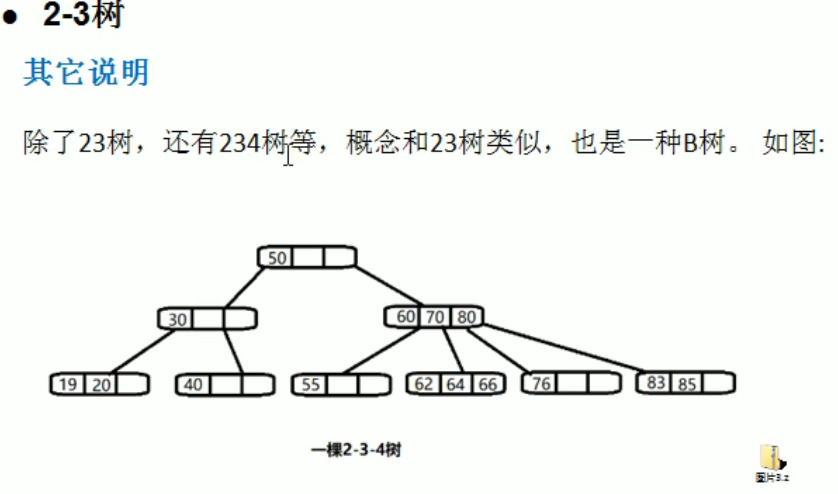

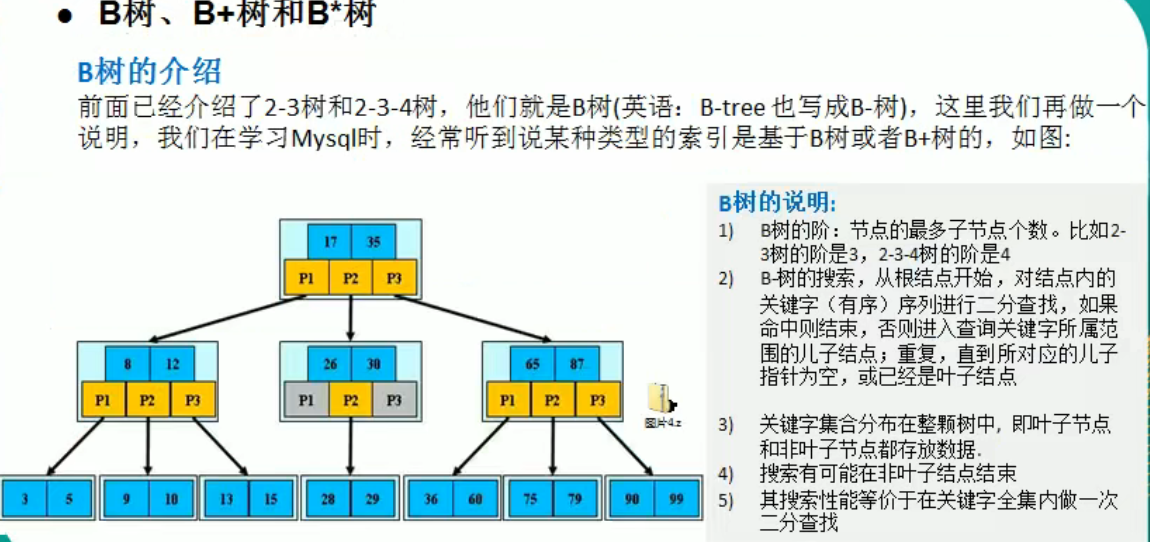
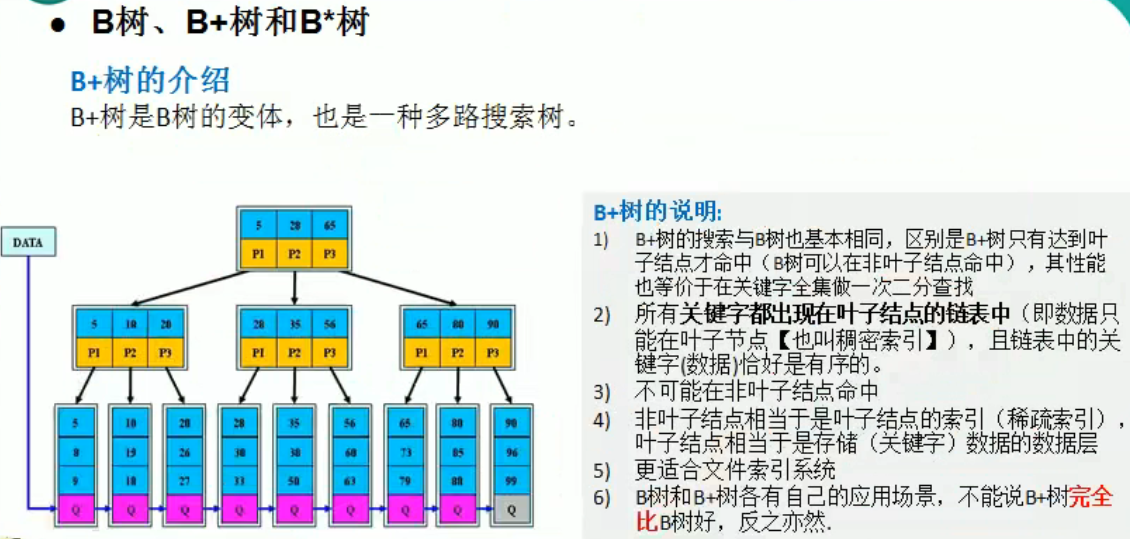
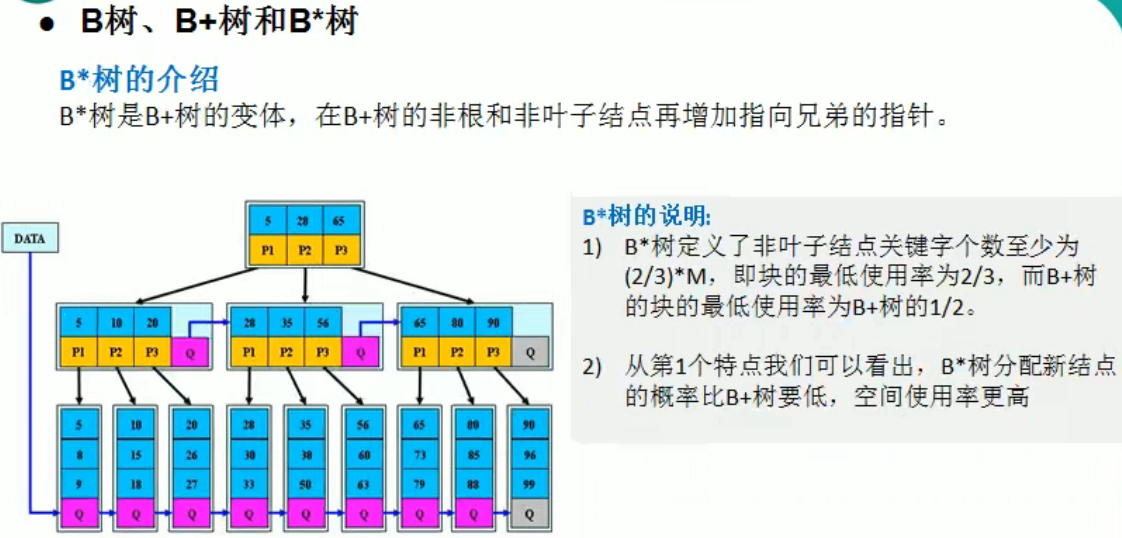
图

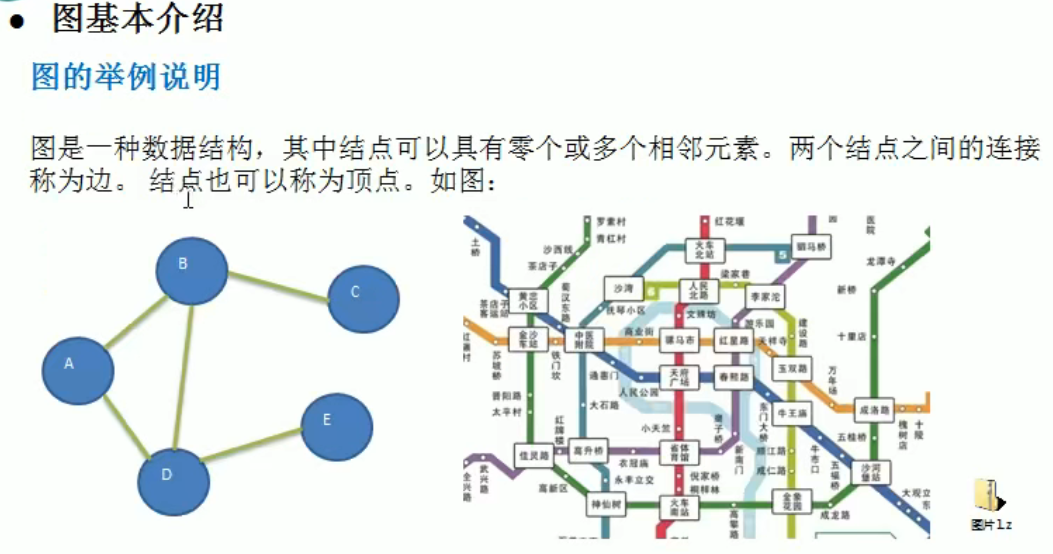
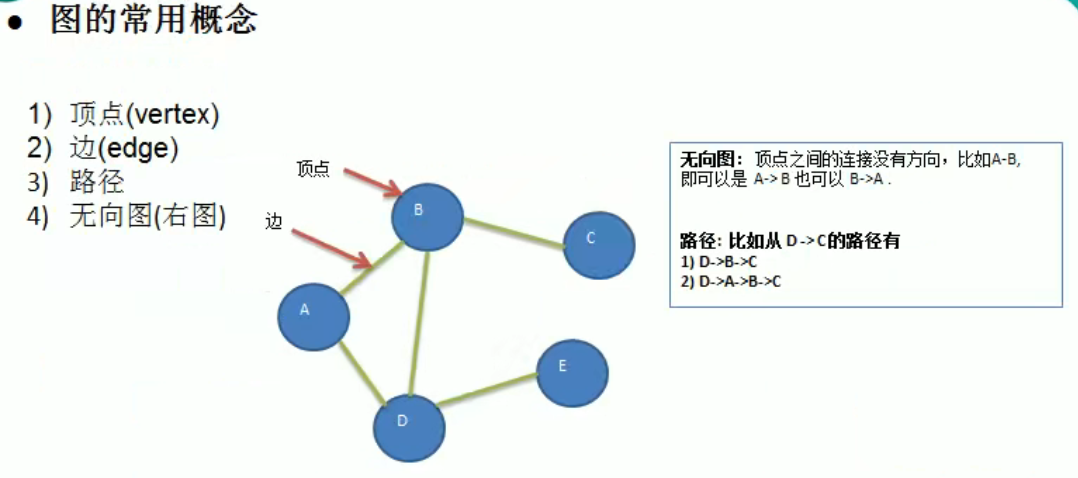
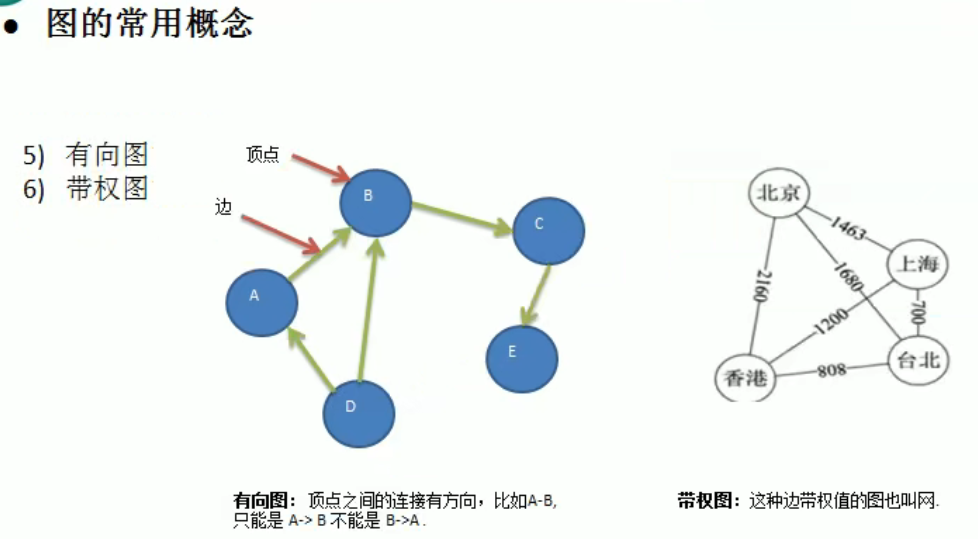
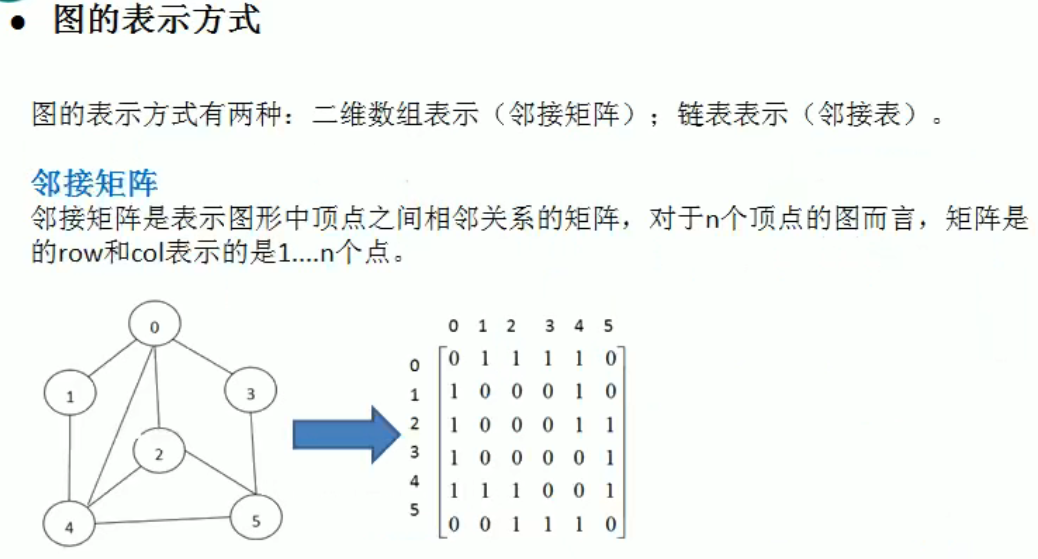
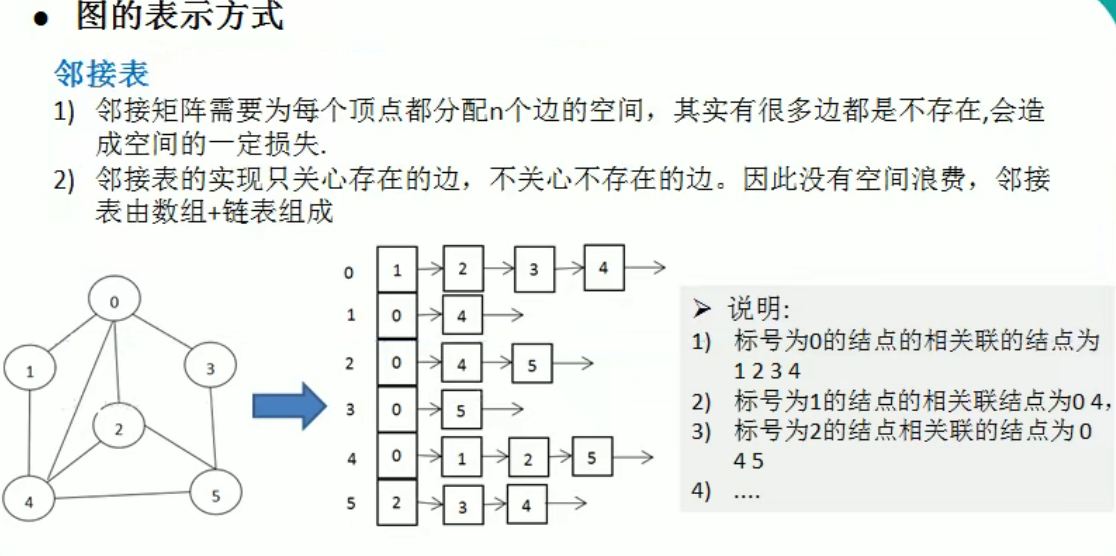
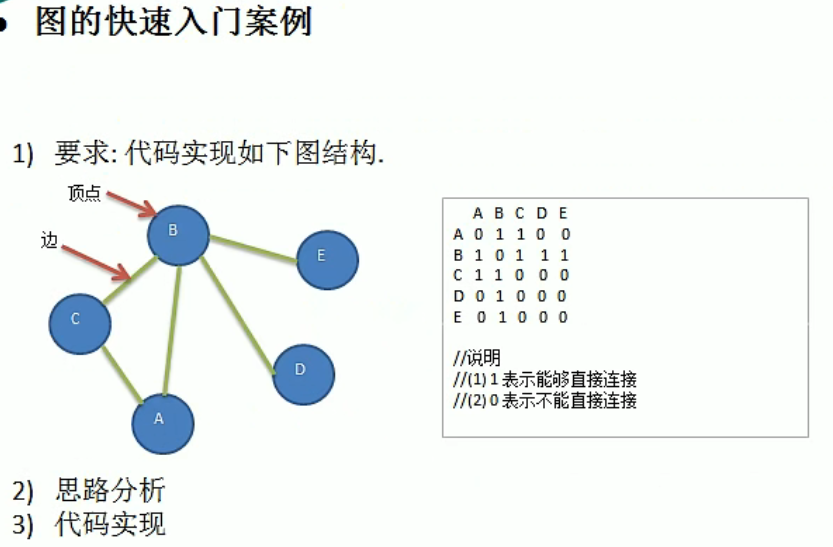
1 | |
深度优先遍历 DFS

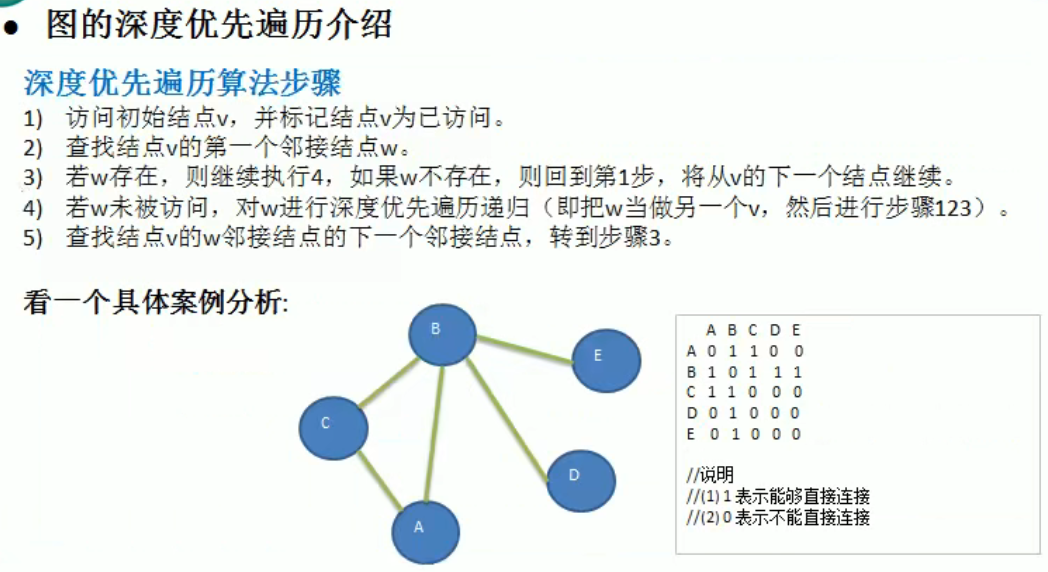
编写思路:
- 访问节点 v ,并标记已访问
- 查找 v 的下一个邻接节点 w, 使用一个函数去获取 w
- 如果 w 没有被访问过,就递归访问 w,查找 w 的下一个邻接节点
- 如果 w 访问过(由3可知 w 及其 w 邻接之后的点都已经被访问过了),访问与 v 邻接的下一个节点,从 v 的第一个邻接节点开始往后找,如果下一个邻接被访问,就再从下一个邻接开始找,直至找到或者所有都被访问完了。
- 如果找的 v 的下一个邻接,即递归访问 v 的下一个邻接。
1 | |
Method 2:
编写思路:
- 分别编写两个函数,一个函数处理一个节点的,并对其进行深度优先搜索,另一个函数遍历所有节点检查未被处理的函数
1 | |
广度优先搜索 BFS

编写思路:
- 输出当前节点并标记
- 将当前节点存入带邻接队列
- 先从队列中取出当前节点,然后找其邻接节点
- 循环获取当前节点的邻接节点,然后入队
- 当前邻接节点全部入队完之后,对其邻接节点再次寻找邻接节点,直至队列空。
1 | |
十个常用算法
二分查找(非递归)

1 | |
分治算法



汉诺塔


1 | |
动态规划算法
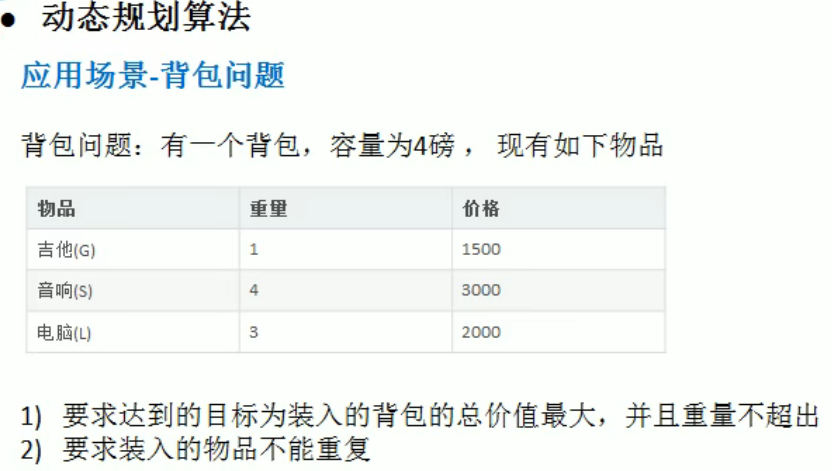



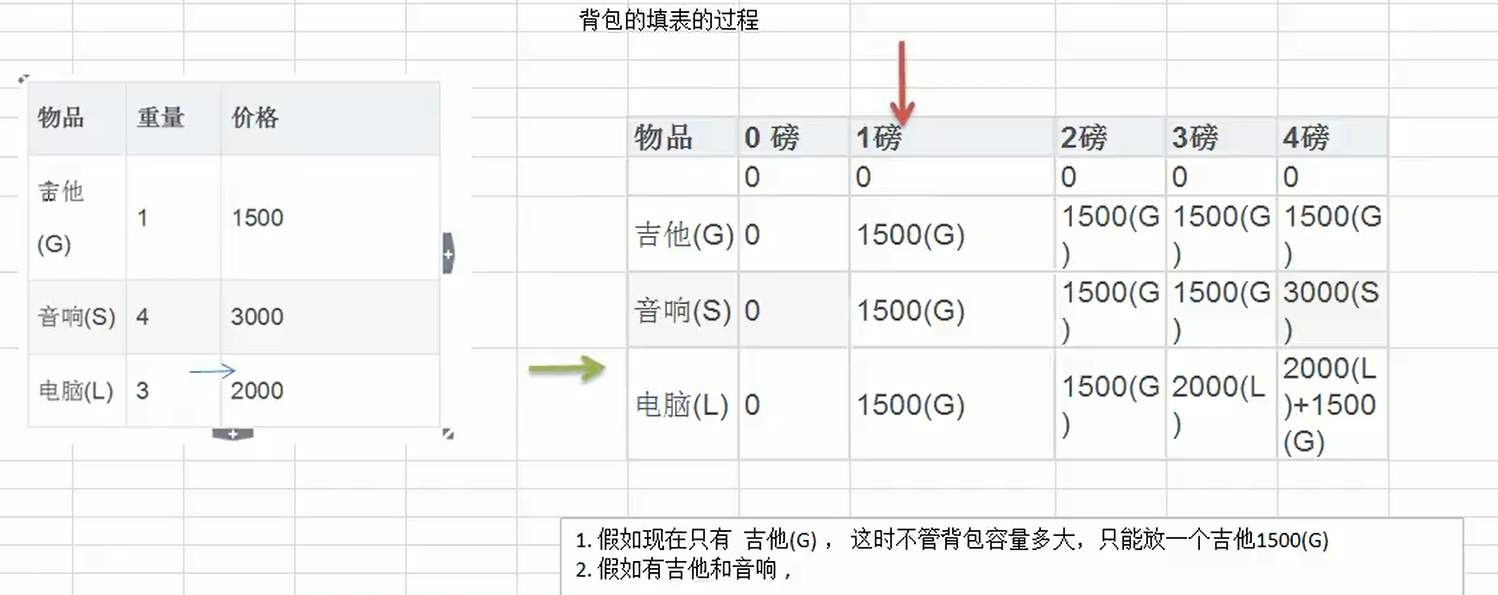
1 | |
KMP 算法

暴力匹配

1 | |
KMP



如何找到部分匹配表







1 | |
贪心算法



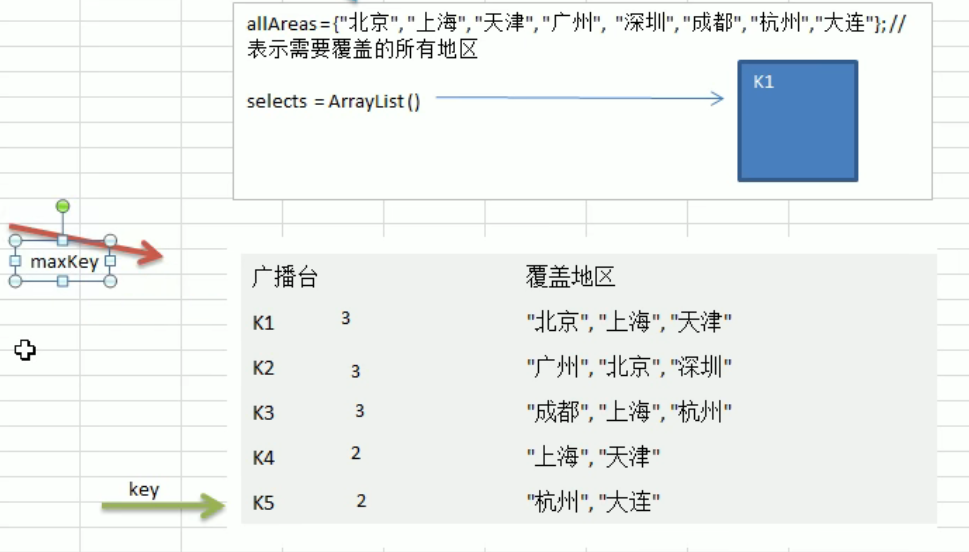
编写思路:
- 为不同广播覆盖位置创建 key-value 的 map HashMap<String, HashSet/
> - 获得所有地区的集合
- 每次循环比较不同广播台的地区与所有地区获取其交集,并在一次循环中获取最大的交集数的广播台放入到 一个 list 中
- 并再所有地区集合中清除该广播台覆盖区域
- 最终 list 就获得每次循环的最优解即为最终解
1 | |
普利姆算法 Prim
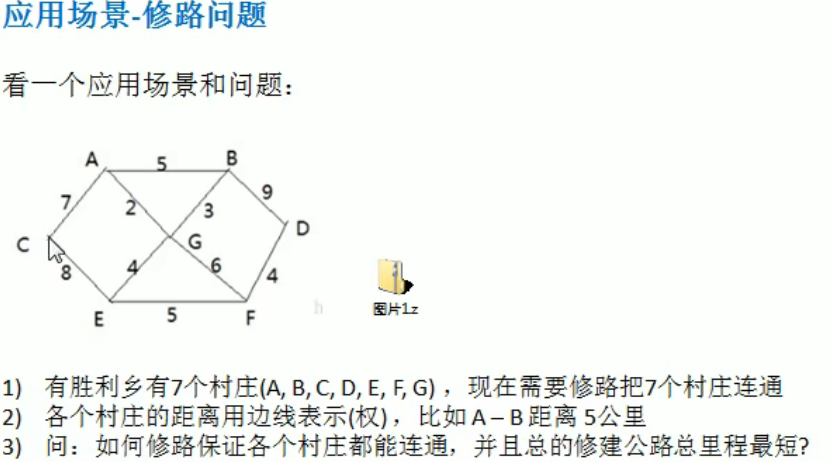
尽可能选择少的路线,并且每条路最小,保证总里程数最少
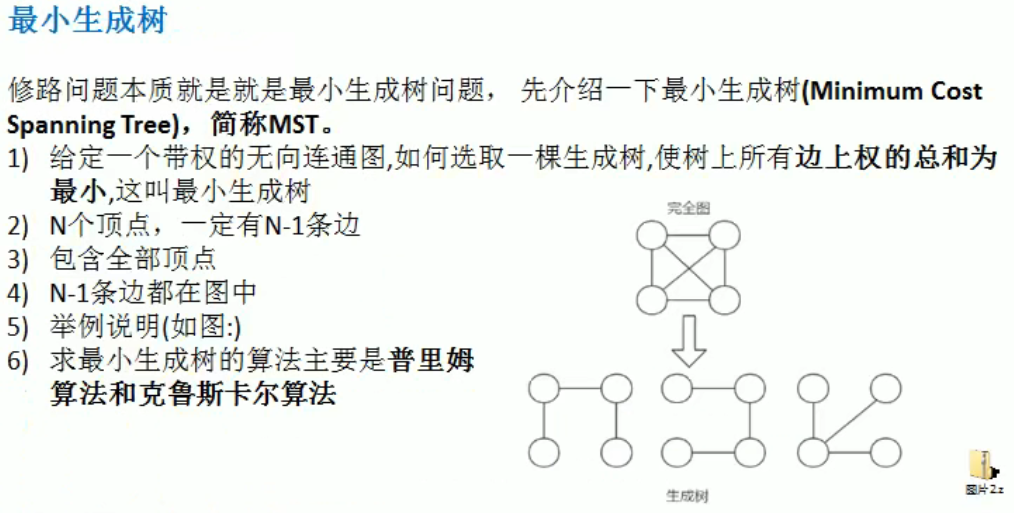


1 | |
克鲁斯卡尔算法 Kruskal
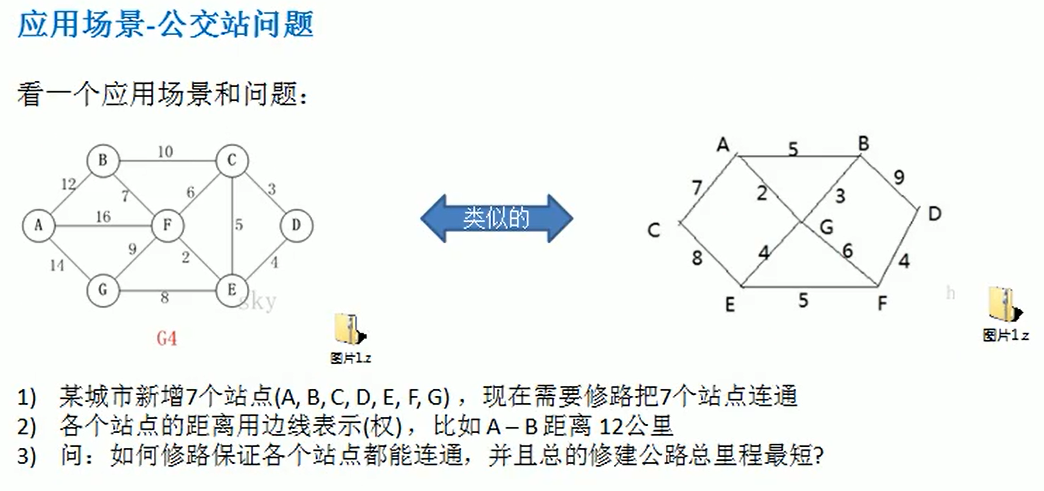

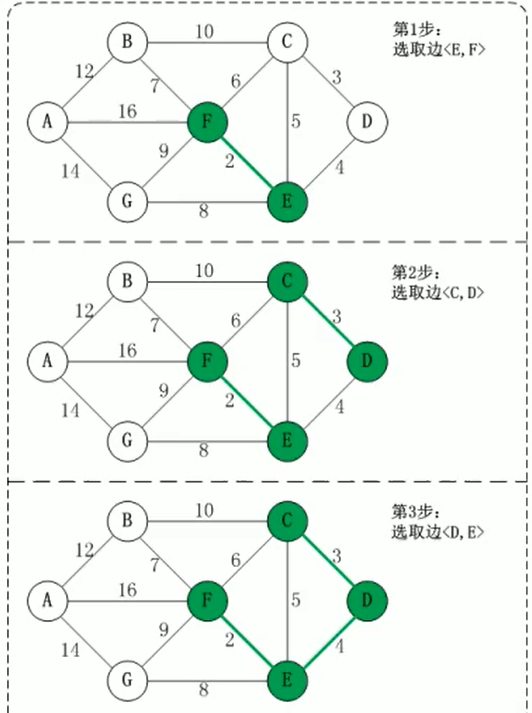
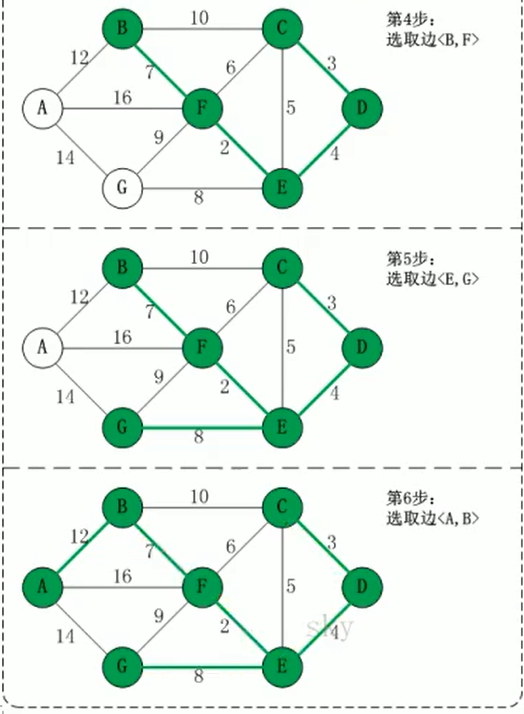


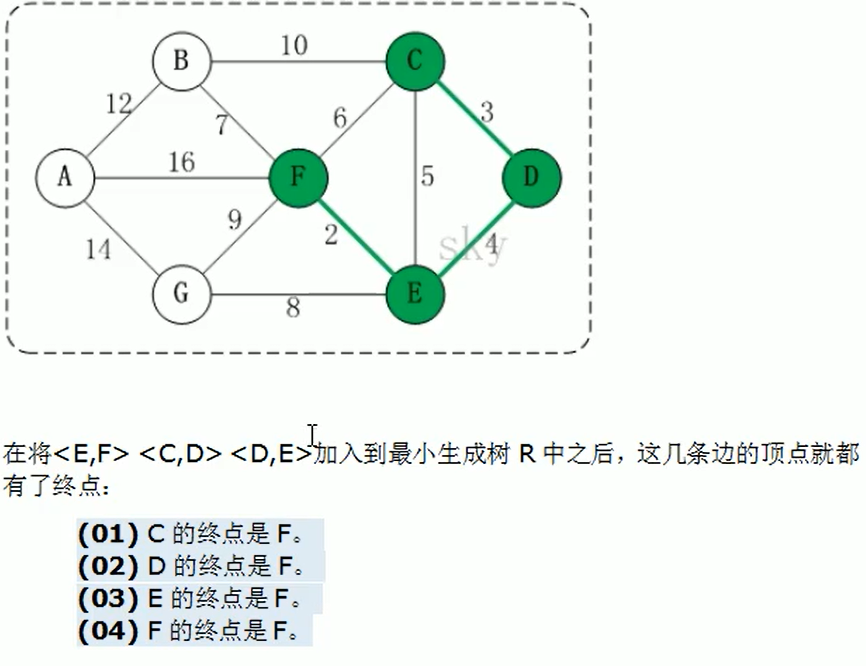

编写思路:
- 获取矩阵的边
- 对边排序
- 设置动态数组 ends 及其函数,记录每次加入新的边时,获取该边的两个节点 i, j (char 比较 i < j)的终点值,然后对比,如果不同就不形成回路,更新 ends 即 char 小的节点下标指向 char 大的节点 ends[i] = j;
- 并将当前节点放入结果数组中。
1 | |
迪杰斯特拉算法 Dijkstra
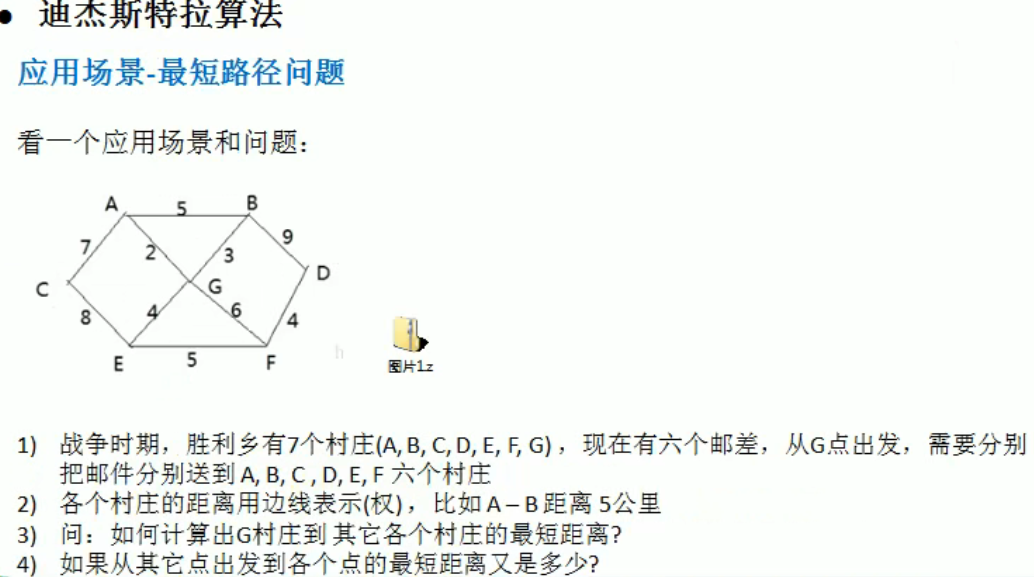


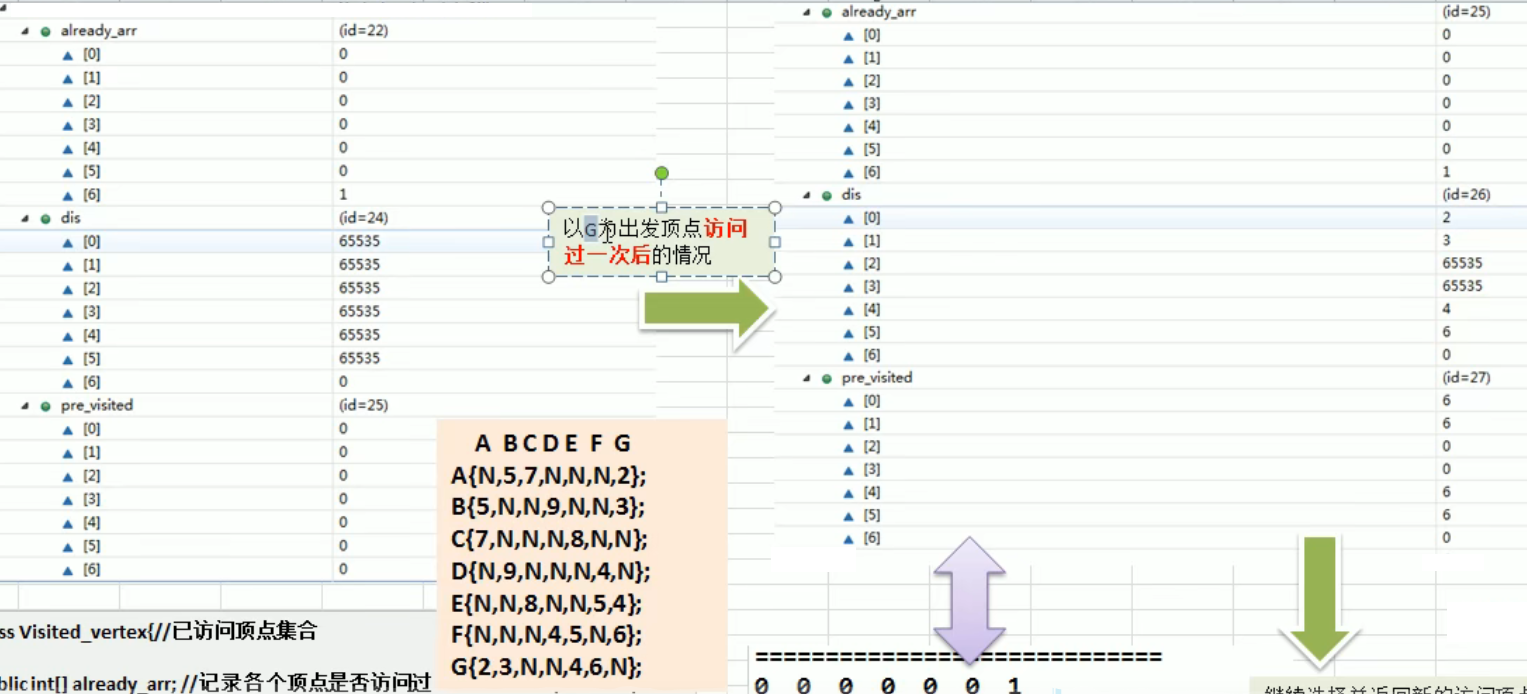
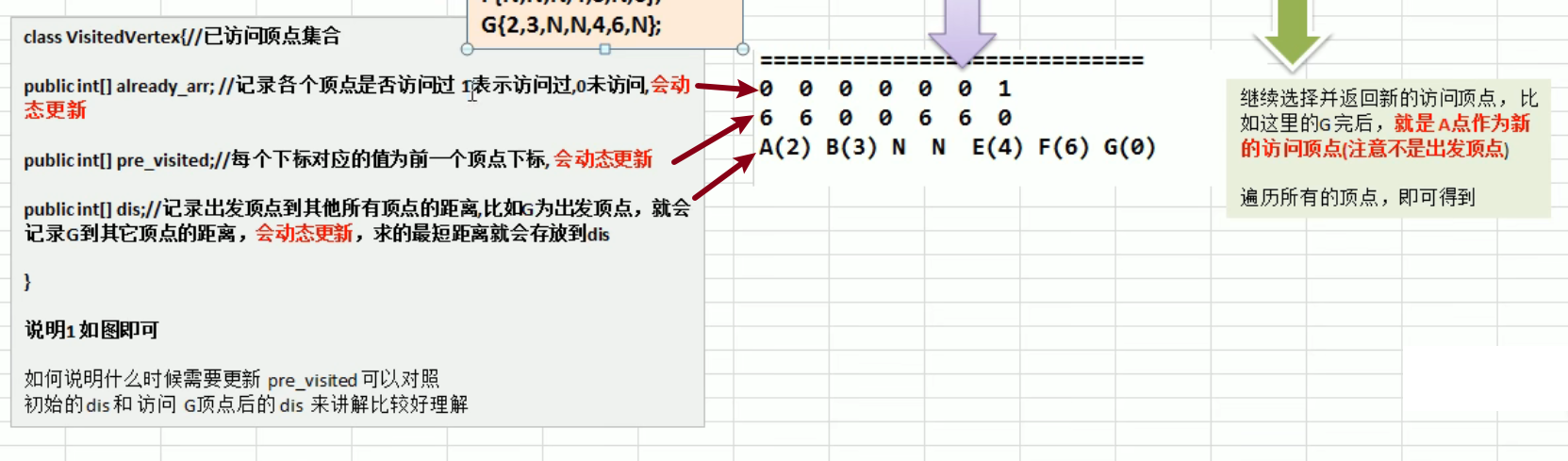
编写思路:
- 构建 VisitedVertex 类,并初始化每个属性
- 写辅助函数用于更新 already_arr,pre_visitied (可以获得两点之间最短的路径见代码结果), dis 的值
- 写一个函数调用上面的更新方法
- 由于节点距离需要累加 如 G->D (i) 要经过 A(index) len = visitedVertex.getDis(index) + matrix/[index][i];
- 更新前驱节点和距离
- 对于一个节点完成之后,写一个函数寻找它最近的节点
- 再用最近的节点去更新 already_arr,pre_visitied, dis 的值
1 | |
弗洛伊德算法(Floyd)


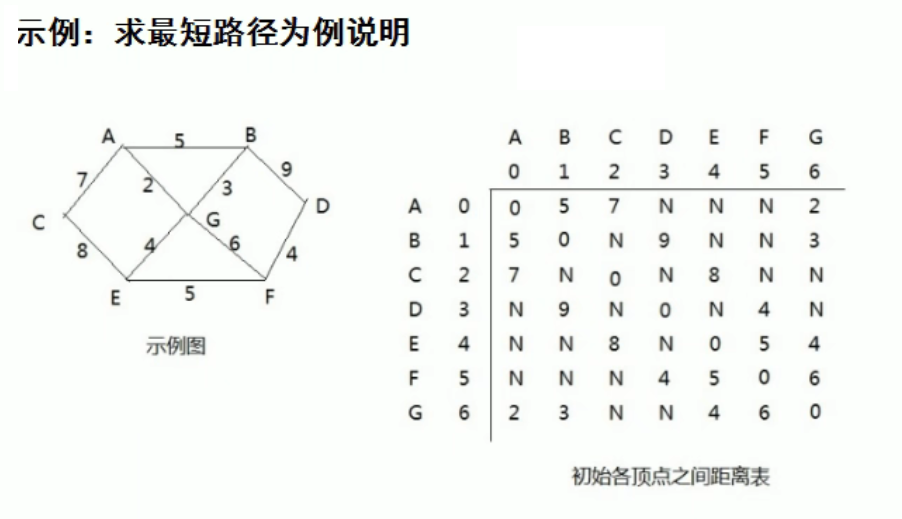
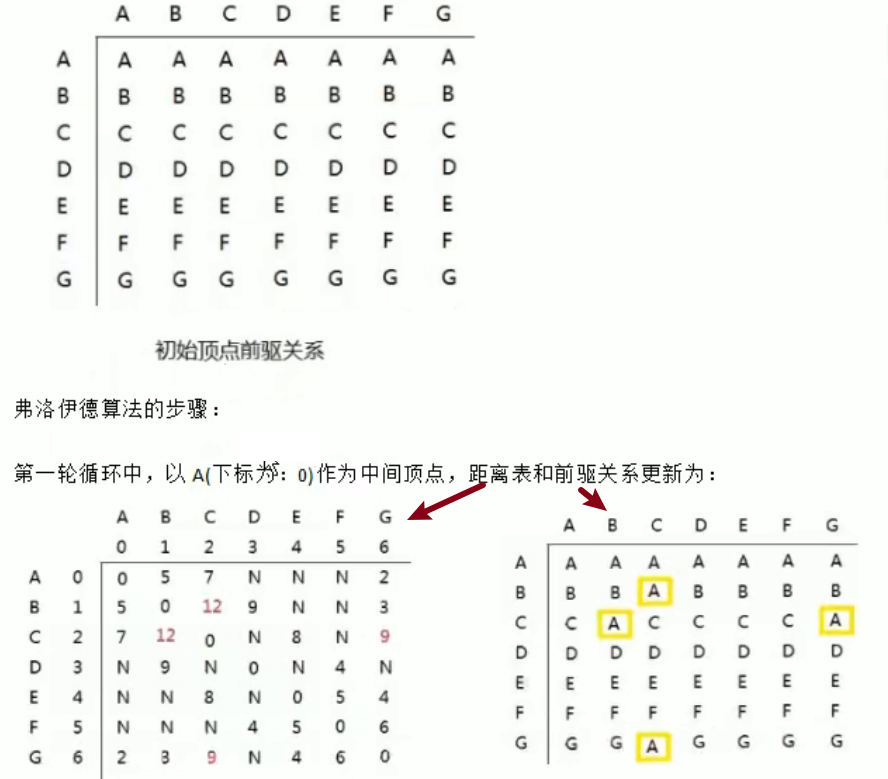
中间顶点 [ A, B, C, D, E, F, G ]
出发顶点 [ A, B, C, D, E, F, G ]
终止顶点 [ A, B, C, D, E, F, G ]
以 A 为中间顶点,遍历 A 为出发顶点时的终止顶点,直至遍历完所有的出发顶点,然后遍历下一个中间节点直至结束

1 | |
骑士周游
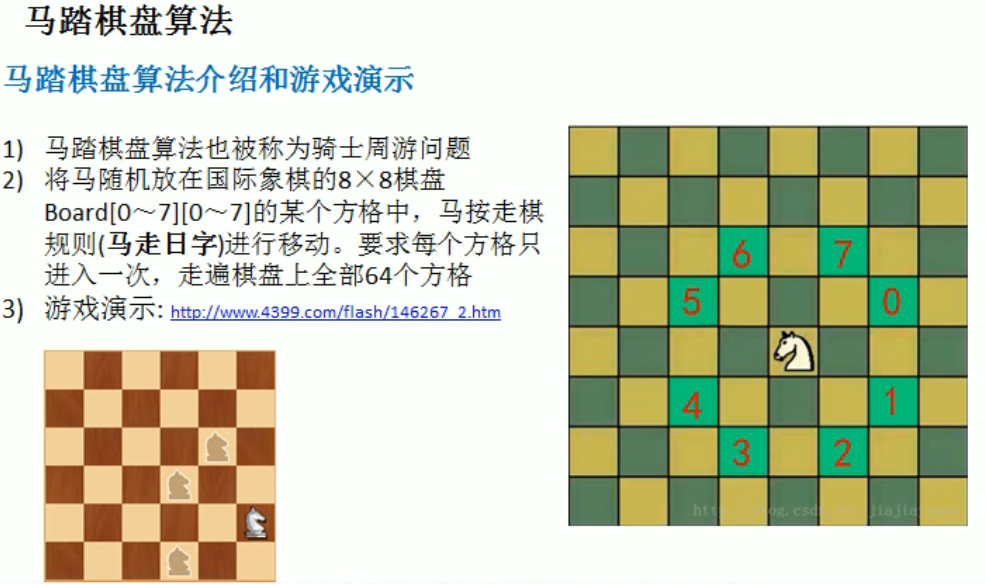

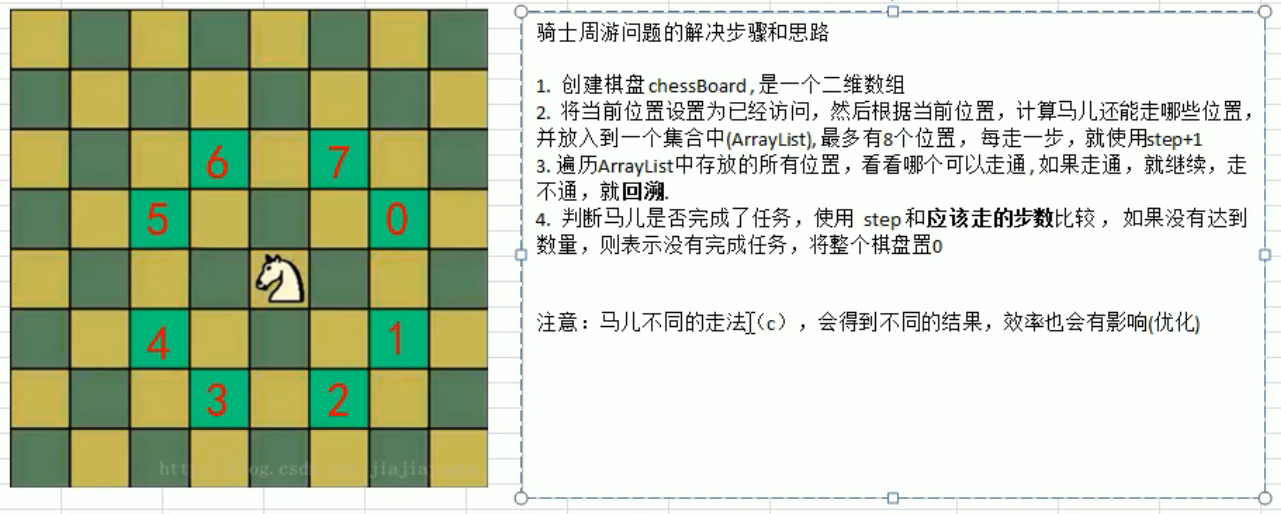
编写思路:
- 使用 next 函数获取当前节点可以走的下一步节点的集合
- 递归集合中的节点
- 当集合中的节点发现无路可走时, step < 棋盘格子数,就需要重设当前格子为未走过,以便之后其他路径可以选择当前格子
- 如果遍历结束,step == 棋盘格子数,设置变量 finish 已经完成, if( step < X * Y && !finished )
- 由于 step < 棋盘格子数 有两种情况 1. 没有完成 2. 处于回溯之中,为了保证处于回溯中的数据不被修改 !finished 在完成之后就会变成 false 就不会去重设当前格子。
1 | |
贪心算法优化

马儿走的下一步是下一步集合中数目最少的从而减少回溯的次数。
1 | |