Code Daily (1)

Code Daily

剑指 Offer 03. 数组中重复的数字

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：

[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 

限制：

2 <= n <= 100000

我的方法（没有看清题目，误以为数字的大小包含了负数，以下是对于包含负数的解）：

1. 如果包含负数，就不能用数组的 index 去映射数字（index） 到次数这层关系
2. 此处需要映射，所以用了 Map
3. 先初始化 value 的值为 0 ，因为是 Integer 类型初始值是 null
4. 然后再次遍历该数组，对于相同的 key 的 value 做 + 1 操作
5. 当前 key value 值大与 1 ，说明出现超过一次，就退出返回目标值

Code：

class Solution {
    public int findRepeatNumber(int[] nums) {
        HashMap<Integer, Integer> map = new HashMap<>();
        int target = 0;
        for(int i: nums){
            map.put(i,0);
        }
        for(int i: nums){
            int temp = map.get(i) + 1;
            map.put(i,temp);
            if(map.get(i)>1){
                target = i;
                break;
            }
        }
        return target;
    }
}

Method 2 ( Map )（ num of nums is in 0~n-1 ）Time O(n), Space O(n) :

1. Because the num of nums is in 0~n-1, I could use the index of array to express the num and the value of the index to represent the times of the num in the nums.

class Solution {
    public int findRepeatNumber(int[] nums) {
        int[] timesArr = new int[nums.length];
        int target = 0;
        for(int i : nums){
            timesArr[i]++;
            if(timesArr[i]>1){
                target = i;
                break;
            }
        }
        return target;
    }
}

For the problem we should think in different situation Time Complexity or Space Complexity

Method 3 ( Sort ) Time O( nlogn ) Space O(1):

1. Before finding, I could sort() the nums firstly.
2. To traverse the nums, if there are numbers which are neighbor and equal, the number is target

code:

class Solution {
    public int findRepeatNumber(int[] nums) {
        Arrays.sort(nums);
        for(int i = 1; i < nums.length; i++){
            if(nums[i-1] == nums[i]){
                return nums[i];
            }
        }
        return -1;
    }
}

Method 4 (Map and using the array of nums) Note: the Problem told me the numbers in nums is small than the length the nums.

Time O( n ) Space O(1);

1. the Problem told me the numbers in nums is small than the length the nums.
2. swap the value of nums by represent the value as the index in the nums (nums[nums[i]] = nums[i] )
3. during swaping, if I find the value v1 which index is nums[i] equal to the value v2 which index is i, there are two times for the v1 in the nums.

class Solution {
    public int findRepeatNumber(int[] nums) {
        for(int i = 0; i<nums.length; i++){
            while(nums[i]!=i){
                if(nums[nums[i]] == nums[i]){
                    return nums[i];
                }
                int temp = nums[nums[i]];
                nums[nums[i]] = nums[i];
                nums[i] = temp;
            }
        }
        return -1;
    }
}

剑指 Offer 04. 二维数组中的查找

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

限制：

0 <= n <= 1000

0 <= m <= 1000

Method 1 : Best( Time O ( logn ), Space O( 1 )); Worst ( Time O ( nlogn+m ), Space O)

1. for row, I use binary search.
2. for colunm, I use linear search.

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if(matrix == null){
            return false;
        }
        if(matrix.length == 0){
            return false;
        }
        if(matrix.length == 1 && matrix[0].length == 0){
            return false;
        }
        int rowIndex = 0;
        int i = matrix[0].length-1;//row
        int j = 0; //column
        int k = 0;
        do{
            rowIndex = binarySearchRow(matrix[k],target,i);
            //when the index < 0, the number is small the any numbers in the arr
            if(rowIndex < 0){
                return false;
            }else if(target == matrix[k][rowIndex]){
                return true;
            }else{
                i = rowIndex;
            }
            while(j < matrix.length){
                if(target == matrix[j][i]){
                    return true;
                }else if(target < matrix[j][i]){
                    k = j;
                    break;
                }
                j++;
            }
            if(j == matrix.length || (i == 0 && matrix[j][i] != target) ){
                return false;
            }
        }while(true);

    }

    public int binarySearchRow(int[] arr, int target, int r){
        int left = 0;
        int right = r;
        int mid = 0;
        while(left<=right){
            mid = (left + right) / 2;
            if(target == arr[mid]){
                return mid;
            }else if(target < arr[mid]){
                right = mid-1;
            }else if(target > arr[mid]){
                left = mid + 1;
            }
        }
        return right;
    }

}

Method 2 : Time O (n+m) Space O (1)

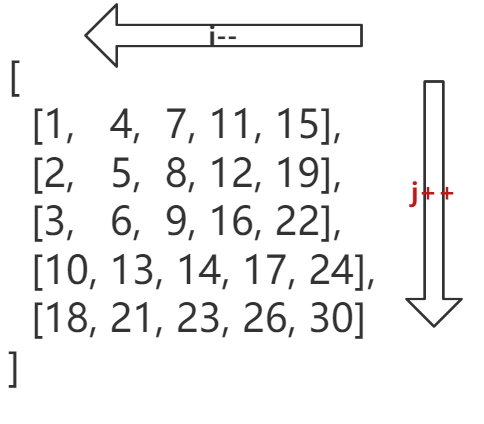
1. I could look at the matrix from its top-right point
2. when it the target is smaller than the number, move to left
3. when it the target is bigger than the number, move to down

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if(matrix == null){
            return false;
        }
        if(matrix.length == 0){
            return false;
        }
        if(matrix.length == 1 && matrix[0].length == 0){
            return false;
        }
        int i = matrix[0].length-1;//column
        int j =0;//row
        while(i>=0&&j<matrix.length){
            if(matrix[j][i] == target){
                return true;
            }else if(target < matrix[j][i]){
                i--;
            }else if(target>matrix[j][i]){
                j++;
            }
        }
        return false;
    }
}